תרגיל דוגמה 17
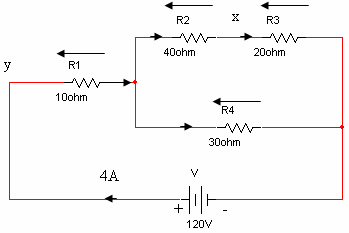
נתון המעגל שבאיור 3.28
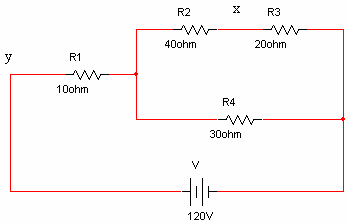
איור 3.28
חשבו את:
א. עצמת הזרם הכללית
ב. ההספק בנגד R3
ג. הזרם דרך הנגד R4
ד. הפרש המתחים Uxy
פתרון תרגיל דוגמה 17
בתרגילים שבהם נתונים כל ערכי הנגדים ומתח המקור, הפתרון מתחיל
בחישוב ההתנגדות השקולה.
את ההתנגדות השקולה נציג כך:
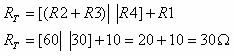
משמעות הביטוי: הנגדים R2 ו- R3 מחוברים בטור, ואליהם מחובר במקביל הנגד R4. בטור לכל הנגדים האלה מחובר R1. הסימן || מבטא חיבור מקבילי, ואילו הסימן + מבטא חיבור
טורי.
הערה:
אם ההצגה הזאת אינה ברורה, יש
לפעול בשלבים כפי שתואר בתרגיל דוגמה 16.
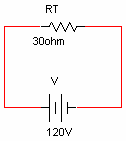
על הנגד RT מופיע מתח המקור. על פי חוק אום נחשב את הזרם
דרך הנגד השקול:
א.
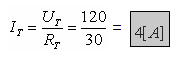
ב. נסמן על המעגל המקורי את עוצמת הזרם הכללית, את כיווני הזרמים
דרך כל נגד ואת קוטביות המתחים:
אפשר לראות שגם דרך הנגד R1
זורם A4. נחשב על פי חוק אום את המתח על פניו:
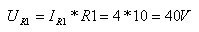
במידה ואין עוד נגדים שאפשר לחשב עליהם מתח וזרם (כדוגמת הנגד R1), יש להפעיל את חוקי קירכהוף במעגל (זו שיטת
פתרון אחת מבין כמה).
נזכיר שחוק הזרמים של קירכהוף מתייחס לצמתים במעגל, ואילו חוק
המתחים של קירכהוף מתייחס לחוגים סגורים במעגל.
במעגל יש שלושה חוגים סגורים שאפשר ליישם בהם את חוק המתחים של
קירכהוף.
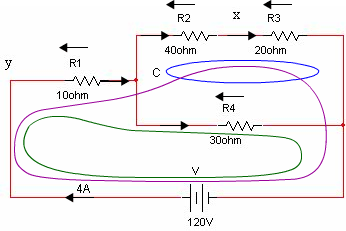
נתבונן בחוג הסגור שמכיל את מקור המתח, הנגד R1 והנגד R4 (חוג בצבע ירוק):
על פי חוק המתחים של קירכהוף מתקיים:
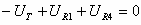
או בדרך נוספת: סכום כל מפלי המתח על פני הנגדים בחוג סגור הכולל
מקור מתח שווה למתח המקור.
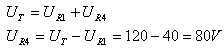
כעת אפשר לחשב את הזרם דרך הנגד R4:
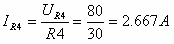
נבדוק שוב אם יש עוד נגדים שאפשר לחשב עליהם מתח וזרם (כדוגמת הנגד
R1 ו- R4).
אם אין, יש להפעיל שוב את חוקי קירכהוף במעגל.
ניסיון להפעיל את חוק המתחים של קירכהוף בשני החוגים האחרים של
המעגל, לא יתרום להמשך הפתרון. וזאת משום שתמיד תתקבל משוואה עם שני נעלמים.
לכן נשתמש בחוק הזרמים של קירכהוף על צומת C:
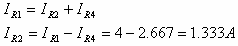
אפשר לחשב את ההספק בנגד R3
כפי שנדרשנו בשאלה:
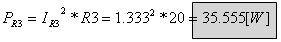
ג. את הזרם דרך הנגד R4 חישבנו
קודם לכן:
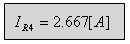
ד. כדי לחשב את הפרש המתחים
בין הנקודותx ו- y, יש "לטייל" מנקודה x לנקודה y ולאסוף מתחים בדרך (ניתן לחשב
זאת בכל מסלול אפשרי):
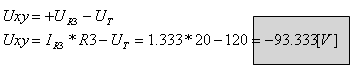
משמעות תוצאה זו:
הפוטנציאל בנקודה y גבוה מן הפוטנציאל בנקודה
x.
כלומר, במידה ונחבר צרכן בין שתי הנקודות הללו, הזרם דרך הצרכן יזרום מנקודה y
לנקודה x (מן הפוטנציאל הגבוה
לפוטנציאל הנמוך).
תרגיל דוגמה 18
נתון המעגל שבאיור 3.29.
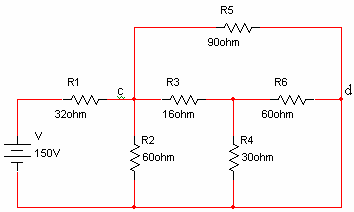
איור 3.29
חשבו את:
א. ההספק הנמסר על ידי מקור המתח
ב. הזרם דרך הנגד R6 וכיוונו
ג. Ucd
פתרון תרגיל דוגמה 18
א. ראשית נחשב את ההתנגדות השקולה של המעגל:
מומלץ לשרטט את המעגל קצת אחרת (כמובן מבלי לשנות את צורת חבור
הנגדים), וזאת כדי לראות בבירור את אופן חיבורי הנגדים:
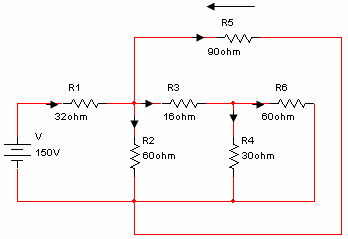
נרשום את ביטוי ההתנגדות השקולה של המעגל:
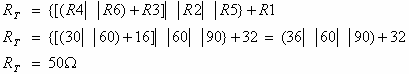
את ההספק הנמסר על ידי מקור המתח אפשר לחשב כך:
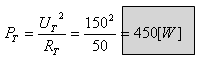
ב. נחשב תחילה את הזרם הכללי במעגל:
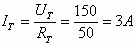
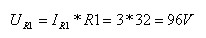
אם אין עוד נגדים שאפשר לחשב עליהם מתח וזרם (כדוגמת הנגד R1), יש להפעיל את חוקי קירכהוף במעגל. על פי
חוק המתחים של קירכהוף מתקיים:
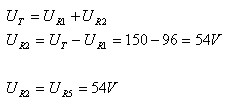
כעת אפשר לחשב זרמים דרך הנגדים האלה:
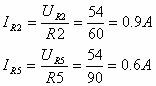
נבדוק שוב האם יש עוד נגדים שאפשר לחשב עליהם מתח וזרם (כדוגמת
הנגד R2 ו- R5). אם אין, יש להפעיל שוב את חוקי קירכהוף במעגל.
על פי חוק הזרמים של קירכהוף:
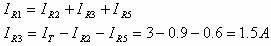
מאחר שהנגדים R4 ו- R6 מחוברים במקביל, אפשר להפעיל עליהם את כלל
מחלק הזרם:
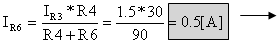
ג. כדי לחשב את הפרש המתחים בין הנקודות c
ו- d, יש "לטייל" מנקודה c
לנקודה d בכל דרך אפשרית, ולאסוף
מתחים בדרך. הדרך הקצרה ביותר היא:
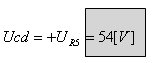
תרגיל דוגמה 19
במעגל שבאיור 3.30 מתפתח בנגד R3 הספק בשיעור w300.
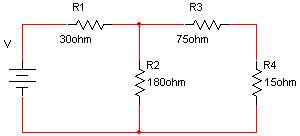
איור 3.30
חשבו את:
א. מתח המקור
ב. זרם דרך הנגד R2
ג. מחברים נגד נוסף במקביל לנגד R2. כתוצאה מחיבור נגד זה, מקור המתח
מספק זרם של 3.5A למעגל. מהו גודלו של הנגד
שחובר?
פתרון תרגיל דוגמה 19
א. בתרגילים מסוג זה, כשחסרים נתונים (כמו למשל מתח המקור), הפתרון
מתחיל מאותו רכיב/קבוצת רכיבים שאנו יודעים עליהם יותר מנתון אחד.
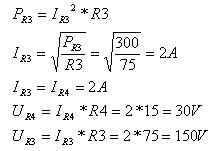
אם אין עוד נגדים שאפשר לחשב עליהם מתח וזרם, יש להפעיל את חוקי
קירכהוף במעגל. על פי חוק המתחים של קירכהוף מתקיים:
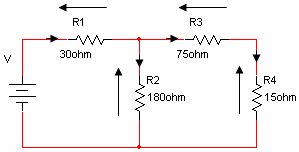
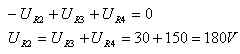
כעת אפשר לחשב את הזרם דרך הנגד R2:
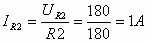
על פי חוק הזרמים של קירכהוף:
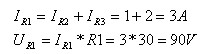
את מתח המקור אפשר לחשב גם על פי חוק אום (מכפלת הנגד השקול בזרם
השקול) וגם על פי חוק המתחים של קירכהוף:
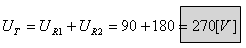
ב.
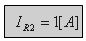
ג. לצורך הפתרון נסרטט את המעגל החדש כך:
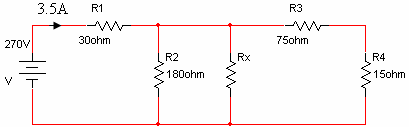
נחשב את המתח בנגד R1:
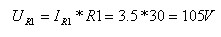
על פי חוק המתחים של קירכהוף:
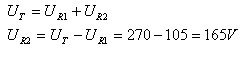
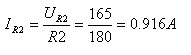
המתח על הנגד R2 שווה גם למתח על פני הנגד
השקול 3,4R, לכן:
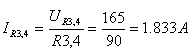
על פי חוק הזרמים של קירכהוף:
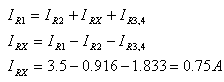
כעת אפשר לחשב את ערכו של הנגד Rx, באמצעות חוק אום:
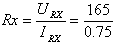
תרגיל דוגמה 20
נתון המעגל שבאיור 3.31. כשהמתג S
סגור, פוטנציאל המתח בנקודה X שווה 60 וולט.
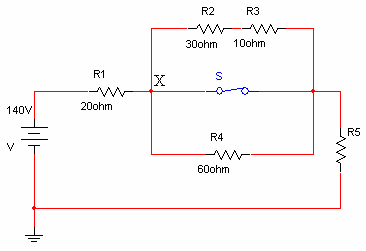
איור 3.31
חשבו את:
א. ערך הנגד R5
ב. פוטנציאל המתח בנקודה X
, כשפותחים את המתג S.
פתרון תרגיל דוגמה 20
הפוטנציאל בנקודה X מוגדר כהפרש המתחים בין
נקודה X לנקודת האדמה. אפשר לחשבו על ידי "טיול" מנקודה X
לאדמה, ואיסוף מתחים בדרך.
כשהמתג סגור מתקבל מעגל
טורי, הנראה כך:
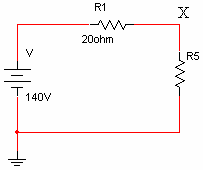
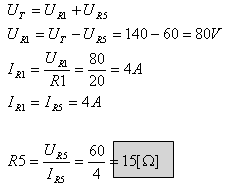
ב. כשהמפסק פתוח הוא אינו משפיע במעגל:
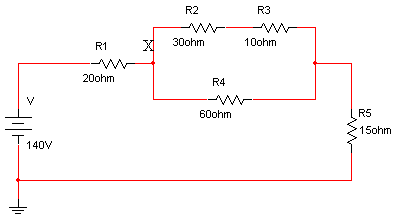
נחשב תחילה את ההתנגדות השקולה שרואה מקור המתח:
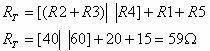
חישוב הפוטנציאל בנקודה X:
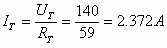
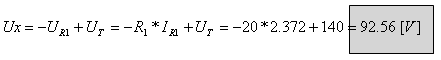
תרגיל דוגמה 21
במעגל שבאיור 3.32 ידוע יחס הנגדים וכן נתון גם הפרש המתחים Uxy=50v.
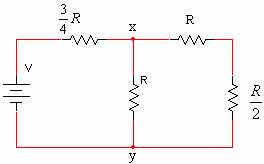
איור 3.32
חשבו את מתח המקור.
פתרון תרגיל דוגמה 21
בתרגילים שבהם ידועים יחסי הנגדים, הפתרון המומלץ יתבסס על כלל
מחלק המתח או על כלל מחלק הזרם.
חשוב לציין, ששימוש בכללים האלה מותנה בצורת חיבור הנגדים. את מחלק
המתח אפשר ליישם בכל ענף טורי של נגדים, ואילו את כלל מחלק הזרם אפשר ליישם אך ורק
על שני נגדים המחוברים במקביל.
כדי ליישם את כלל מחלק המתח במעגל, יהיה עלינו לצמצם את המעגל כך
שיופיעו נגדים בטור.
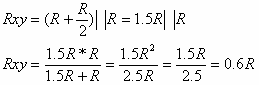
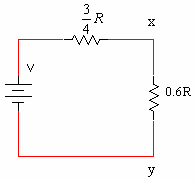
על פי כלל מחלק המתח
מתקיים:
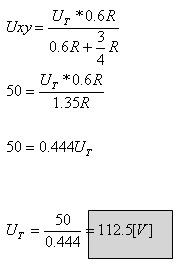
תרגיל דוגמה 22
במעגל שבאיור 3.33 מחובר הנגד (R(q שהוא נגד המשנה את התנגדותו
כתוצאה משינויי טמפרטורה, על פי המשוואה המתמטית:
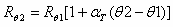
בטמפרטורה של c°35, נמדד דרך הנגד (R(q זרם בשיעור 1.2A.
מקדם הטמפרטורה של
הנגד 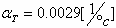
ידוע יחס הנגדים במעגל
כתלות בהתנגדותו של (R(q בטמפרטורה c°35.
הערה: כל הנגדים שמחוברים במעגל הם נגדים קבועים חוץ מנגד (R(q
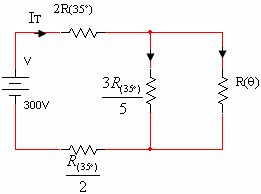
איור 3.33
חשבו את:
א. ערכו של הנגד q)(R בטמפרטורה של c°35;
ב. משנים את הטמפרטורה שבה מצוי המעגל. הזרם המרבי שיכול לספק מקור
המתח הנו 3.5A,
שאם לא כן הוא יינזק. באיזו טמפרטורה המעגל יכול להימצא בלי שייגרם לו כל נזק?
פתרון תרגיל דוגמה 22
א. בחלקו הראשון של הפתרון, נתייחס לעובדה שהמעגל מצוי
בטמפרטורה של c°35 בטמפרטורה זו, אנו יודעים גם את כל יחסי הנגדים במעגל וכן
גם את הזרם דרך הנגד q)(R.
ניעזר בכלל מחלק הזרם כדי למצוא את הזרם הכללי במעגל:
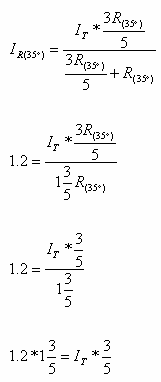
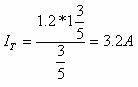
כעת נחשב את ההתנגדות השקולה של
המעגל (בטמפרטורה של c°35):
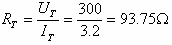
נבטא את ההתנגדות השקולה של
המעגל כתלות בשאר הנגדים (בטמפרטורה של c°35):
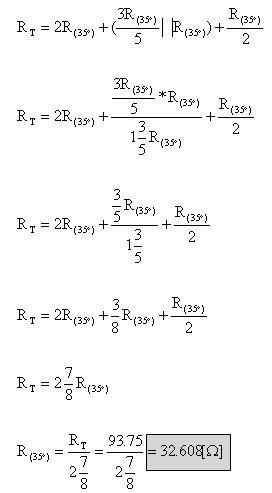
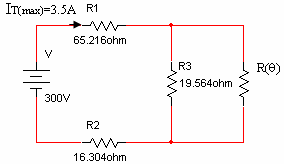
לצורך הפתרון נצייר את המעגל עם כל הנתונים הידועים, בטמפרטורה T
כלשהי:
ראשית נחשב את ערכו של הנגד התלוי בטמפרטורה q)(R:
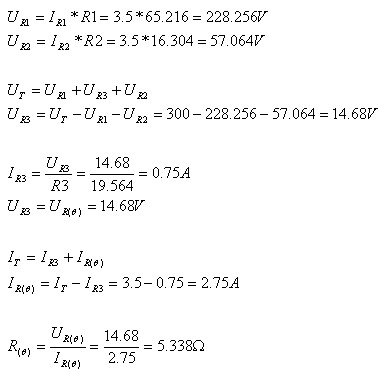
כעת אפשר לחשב את הטמפרטורה
2q שבו מצוי
המעגל:
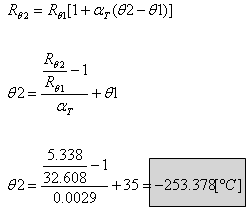
אסור שהמעגל ימצא בטמפרטורה הנמוכה מ- c°235.378-