(Parallel circuit properties)
כדי להסביר את תכונות המעגל המקבילי נתבונן במעגל
שלפנינו
(איור 3.1.1)
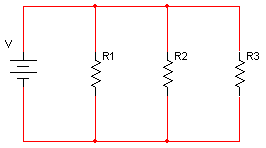
איור 3.1.1
1. המתח על כל אחד מן הנגדים המחוברים במקביל
זהה, ובמעגל המקבילי הוא שווה גם למתח המקור. אפשר לראות שההדק החיובי של המקור
מחובר לכל אחת מן הרגליים העליונות של הנגדים, וכך גם ההדק השלילי מחובר לרגליים התחתונות
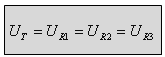
האינדקס T של מתח המקור מציין מתח כללי (Total). פירוש הביטוי הוא שמתח המקור
שווה למתח על פני הנגד R1, וגם שווה
למתח על פני הנגד R2, ולמתח שעל פני הנגד R3.
2. האלקטרונים שיוצאים מהדקו
השלילי של המקור מתפצלים דרך כל אחד מן הנגדים ולבסוף שוב חוזרים באותה כמות להדקו
החיובי של המקור. כמות האלקטרונים מתארת את גודל המטען החשמלי שעובר בפרק זמן
מסוים, והוא הזרם החשמלי.
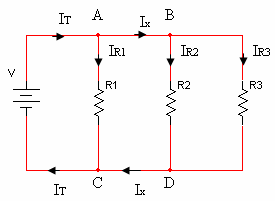
נתבונן שוב בדוגמת המעגל המקבילי
שבאיור 3.1.1 ונסמן תחילה את זרמי המעגל:
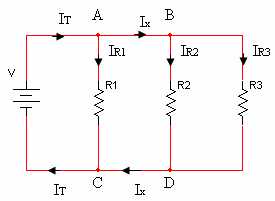
נגדיר כמה מושגי יסוד החשובים להמשך הבנת הנושא:
א. צומת – נקודת מפגש של
שני מוליכים לפחות, שזורם בהם זרם. לכל צומת יש "בן זוג". בזוג
צמתים זורמים תמיד אותם זרמים, אך בכיוונים הפוכים. כלומר, אם בצומת אחד הזרם
נכנס, בבן זוגו הזרם יוצא.
אם הזרם Ix נכנס לתוך צומת B(ימינה), מצומת הבן זוג (D)
יצא אותו הזרם Ix (שמאלה).
ב. ענף – קטע המחובר בין שני צמתים.
חוק הזרמים של קירכהוף (Kirchhoff's Current Law)
חוק זה קובע שסכום הזרמים הנכנסים לצומת שווה לסכום
הזרמים היוצאים מאותו הצומת.
את חוק הזרמים של קירכהוף אפשר
לנסח גם כך: סכום הזרמים בצומת שווה לאפס. זרמים הנכנסים לצומת נסמן כחיוביים,
ואילו את הזרמים היוצאים נסמן שליליים. כלומר לא תיתכן הצטברות של מטען בצומת.
מעניין אתכם לדעת מיהו קירכהוף?
לחצו כאן
מאחר שבמעגל יש ארבעה צמתים, אפשר
להפעיל את חוק הזרמים של קירכהוף בכל אחד מארבעת הצמתים.
בעבור צומת B:
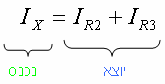
בעבור צומת D:
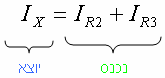
אם נציב במקום הזרם Ix את סכום הזרמים דרך
הנגדים R2 ו- R3, נקבל את היישום של חוק קירכהוף לזרמים
במעגל:
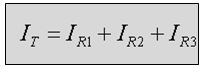
דוגמה נוספת ליישום חוק הזרמים של קירכהוף:
נתון צומת שמחוברים אליו שישה מוליכים שבהם זורם זרם (ראו איור
3.1.2).
חוק הזרמים עבור צומת זה הנו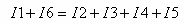
בעבור כל אחד מן הזרמים המתוארים באיור 3.1.2 עליכם לבחור את כיווני הזרמים.
השלימו את
כיווני הזרמים במוליכים השונים.
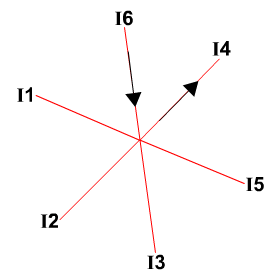
איור 3.1.2
3. נגדי המעגל מהווים בעבור מקור האנרגיה עומס אחד שקול. אפשר להחליף
את שלושת נגדי המעגל המקבילי בנגד אחד שקול RT, כך שעוצמת הזרם היוצא מן המקור לא תשתנה.
הנגד השקול RT במעגל מקבילי, יחושב
באופן הזה:
על פי חוק הזרמים של קירכהוף:
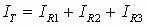
נבטא כל אחד מן הזרמים
על פי חוק אום:
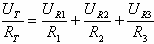
מתח המקור במעגל מקבילי שווה למתח שנופל על כל נגד. לכן אפשר לרשום
זאת כך:
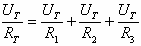
נכפול את כל המשוואה ב-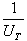 ונקבל:
ונקבל:
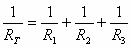
(3.1)
עדיין אין זה ערכו של הנגד השקול. לחישוב הנגד השקול RT נבצע את הפעולה הזאת:
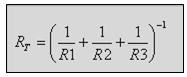
(3.2)
הערה: משוואה 3.1. היא המשוואה לחישוב המוליכות השקולה של המעגל.
כלומר מקור האנרגיה "יראה" נגד אחד שקול שערכו RT:
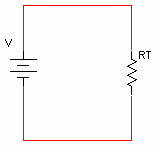
הערות:
א. חישוב התנגדות שקולה בעבור 2 נגדים בלבד המחוברים במקביל
נרשום תחילה את הביטוי הכללי למציאת ההתנגדות השקולה:
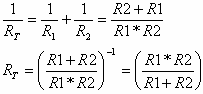
כלומר, בעבור חיבור מקבילי של שני נגדים, אפשר להיעזר בנוסחא 3.3
(מכפלת שתי ההתנגדויות שבמקביל לחלק לסכומן):
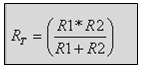
3.3
ב. חישוב ההתנגדות השקולה בעבור n נגדים המחוברים במקביל
לדוגמה, נחבר ארבעה נגדים זהים במקביל (n=4), ונרשום את הנוסחה הכללית לחישוב ההתנגדות
השקולה:
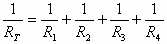
מאחר שהנגדים זהים, אפשר לרשום זאת גם כך:
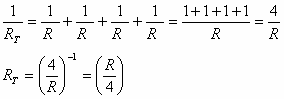
יש לזכור שהמספר 4 הוא מקרה פרטי, אך באופן כללי יצוין מספר הנגדים
הזהים שחוברו במקביל באמצעות הפרמטר n.
לכן, חישוב נגד שקול בעבור
n נגדים
זהים במקביל יחושב:
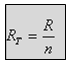
3.4
ג. ההתנגדות השקולה RT – חייבת להיות בעלת ערך
הקטן מההתנגדות הקטנה ביותר בחיבור
המקבילי. ככל שנחבר עוד נגדים במקביל, כן ההתנגדות השקולה תלך ותקטן.
4. האנרגיה וההספק הכוללים במעגל
שווה לסכום האנרגיות, או ההספקים, הנצרכים על ידי כל נגדי המעגל. על סמך מעגל הדוגמה שמתואר באיור 3.1.1 נקבל:
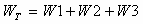
ובעבור הספקים נקבל:
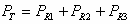
המשוואות האלה תקפות לכל צורת חיבור של נגדים, לאו דווקא חיבור מקבילי.