(Transitional phenomena in DC Circuits - second order circuits)
מעגל הניתן לתיאור על ידי משוואה דיפרנציאלית מסדר שני ייקרא מעגל
מסדר שני. משוואה דיפרנציאלית נקראת מסדר שני אם הנגזרת הגבוהה ביותר המופיעה
במעגל, היא נגזרת שנייה.
לדוגמה: מעגל הכולל קבל
וסליל קרוי בשם מעגל מסדר שני. בעבור המעגלים האלה משוואת הזרם הדינאמית בתקופת
המעבר מכילה שני שורשי S:
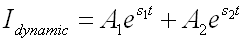
כאשר:
S1,S2–
שורשי המשוואה האופיינית של המעגל
A1,A2– מקדמים קבועים שניתנים לחישוב בעזרת תנאי
ההתחלה (מחושבים במשוואת הזרם הכללית בלבד)
הערה: כדי לקבל פתרון יחיד למשוואה דיפרנציאלית מסדר שני, חייבים להיות
ידועים שני תנאי התחלה.
רישום משוואת הזרם
הכללית:
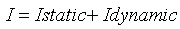
כאשר:
I static – הזרם במצב המתמיד (לאחר זמן
רב)
I dynamic
– הזרם במעגל בתקופת המעבר
הערה: מעגל שמכיל שני קבלים או שני סלילים שאי אפשר לצמצם ביניהם קרוי
אף הוא מעגל מסדר שני.
באיור
15.5 מתואר מעגל RLC
טורי המחובר למקור מתח ישר.
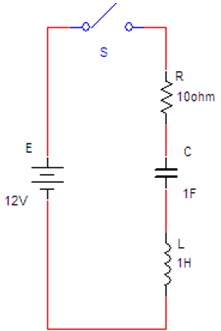
איור 15.5
בשלב
הראשוני נרשום את המשוואה האופיינית של המעגל:
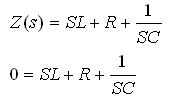
נכפול
את המשוואה ב-SC:
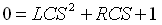
נציב את ערכי הקבל,
הסליל והנגד ונקבל משוואה ריבועית שלה שני שורשים (פתרונות):
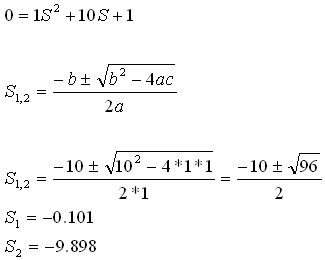
משוואת הזרם הכללית:
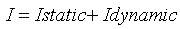
חישוב
הזרם במצב הסטטי (סיום תופעת המעבר) – קבל נתק וסליל קצר:
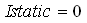
חישוב
הזרם במצב הדינמי:
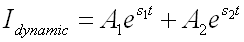
נמצא
את המקדמים A1
ו- A2
בעזרת תנאי התחלה במשוואת הזרם הכללית. בעבור t=0 הזרם במעגל שווה לאפס
(הסליל נתק והקבל קצר):
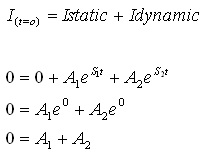
כדי למצוא את ערכי הפרמטרים A1 ו- A2 ניעזר בעוד תנאי התחלה:
ברגע t=0 כל מתח המקור מופיע על
הסליל כי הוא מהווה נתק, ואילו הקבל מהווה קצר. לכן:
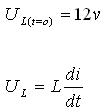
נגזור
את משוואת הזרם הכללית:
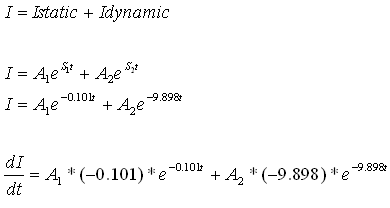
נציב t=0 ונעזר בביטוי:
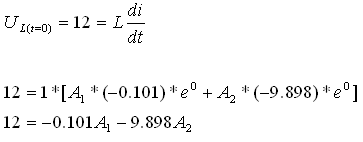
ידוע ש: 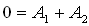 כלומר
כלומר 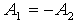
נציב ונקבל:
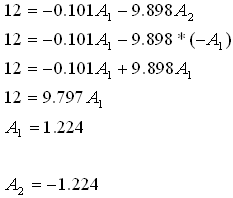
נרשום
את משוואת הזרם הכללית:
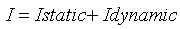
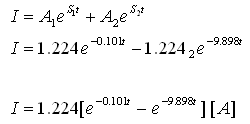
בעזרת משוואה זו, שהתקבלה, אפשר לחשב את הזרם במעגל בכל רגע נתון.
באיור
15.6 מתוארת, באופן עקרוני, השתנות הזרם במעגל מרגע סגירת המתג.
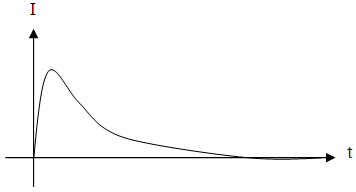
איור 15.6
שינוי ערך הנגד עשוי לשנות את צורת השתנות הזרם, כך שבסופו של דבר
עצמת הזרם תהיה שווה לאפס אך עם תנודות מתרסנות, או שיתקבל אות זרם סינוסי שאינו
מתרסן שרוכב על רמת DC
השווה לאפס.
נשנה את ערכו של הנגד ל- 1W ונבדוק כיצד ישפיע הדבר על אות הזרם במעגל.
נתאר שוב את המשוואה האופיינית של המעגל שמתואר באיור 15.5:
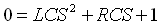
נציב את ערכי הקבל, הסליל והנגד ונקבל משוואה ריבועית שיש לה שני שורשים
(פתרונות):
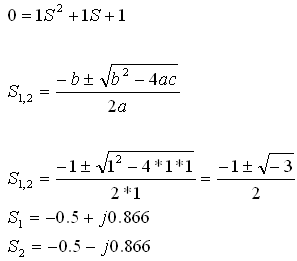
משוואת הזרם הכללית:
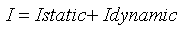
חישוב הזרם במצב הסטטי (סיום תופעת המעבר) – קבל נתק
וסליל קצר:
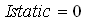
חישוב הזרם במצב הדינמי:
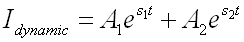
נמצא את המקדמים A1 ו-A2 בעזרת תנאי התחלה במשוואת הזרם הכללית. בעבור t=0 הזרם במעגל שווה לאפס (הסליל נתק והקבל
קצר):
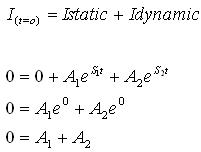
כדי למצוא את ערכי הפרמטרים A1 ו- A2
ניעזר בעוד תנאי התחלה:
ברגע t=0 כל מתח המקור מופיע על הסליל
כי הוא מהווה נתק, ואילו הקבל מהוה קצר. לכן:
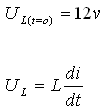
נגזור את משוואת הזרם הכללית:
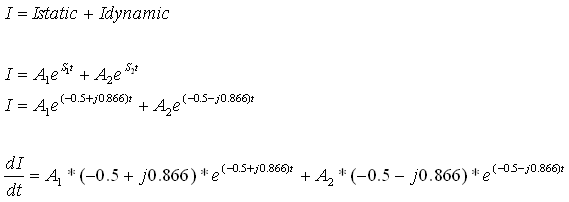
נציב t=0 ונעזר בביטוי:
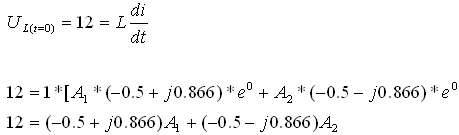
ידוע ש: 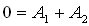 כלומר
כלומר 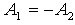
נציב ונקבל:
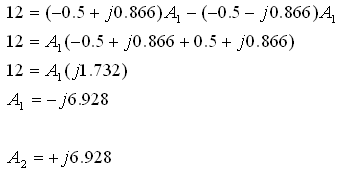
נרשום את משוואת הזרם הכללית:
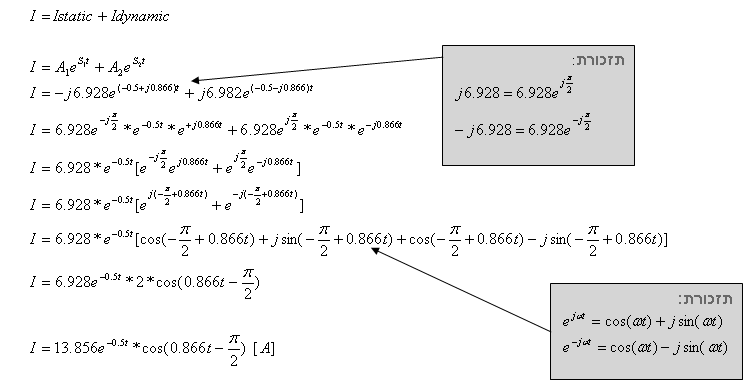
בעזרת משוואה זו, שהתקבלה, אפשר לחשב את הזרם במעגל בכל רגע נתון.
באיור 15.7 מתוארת, באופן עקרוני, השתנות הזרם במעגל מרגע סגירת
המתג – תנודות מתרסנות:
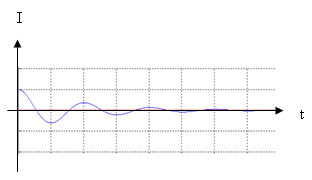
איור 15.7