תרגיל
דוגמה 1
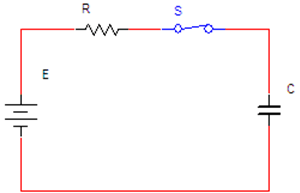
נתון המעגל החשמלי שבאיור 15.5.
ברגע t=0 סוגרים את המתג S.
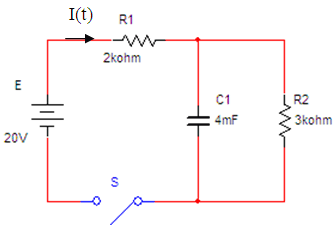
איור 15.5
א. חשבו את עצמת זרם המקור כעבור זמן רב;
ב. רשמו את משוואת הזרם 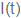
ג. חשבו את המתח על הקבל כעבור 5
שניות מרגע סגירת המתג.
פתרון
תרגיל דוגמה 1
ב. נפעל בהתאם לשלבים שתוארו במעגלים שבאיורים 15.3 ו-
15.4.
שלב ראשון - חישוב 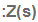
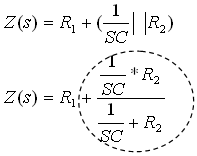
נכפול את המונה והמכנה של הביטוי המקווקו ב- SC ונקבל:
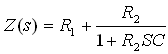
שלב
שני – רישום המשוואה האופיינית ומציאת שורשי המשוואה:
נשווה את הביטוי 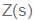 לאפס ונקבל את המשוואה האופיינית:
לאפס ונקבל את המשוואה האופיינית:
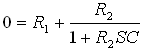
נמצא את שורשי המשוואה האופיינית, כלומר את ערכי S המקיימים את איפוס
המשוואה:
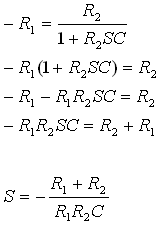
התוצאה שהתקבלה היא קבוע זמן
הטעינה של הקבל. נציב את ערכי R ו- C ונקבל את שורש המשוואה האפיינית:
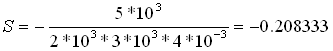
שלב
שלישי – רישום משוואת הזרם הכללית של המעגל:
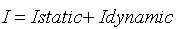
הזרם במצב הסטטי חושב בסעיף א'
ושווה ל- 4mA.
בתקופת המעבר, בעבור מעגל מסדר
ראשון משוואת הזרם הדינמית תירשם כך:
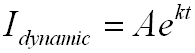
נחשב את A בעזרת המשוואה
הכללית של הזרם (עם תנאי ההתחלה t=0):
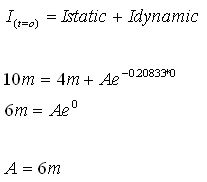
נרשום את משוואת הזרם הכללית:
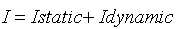
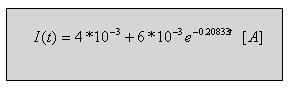
ג. נמצא את זרם המקור כעבור 5
שניות מרגע סגירת המתג:
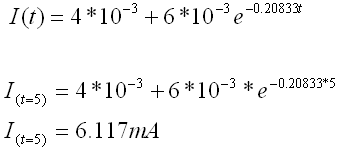
זרם זה עובר גם דרך הנגד R1 ולכן:
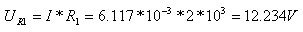
על פי חוק המתחים של קירכהוף:
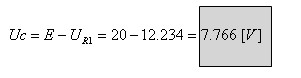
עד כה השתמשנו במישור s למציאת שורשי המשוואה האופיינית
בלבד, אך את שאר הפתרון ביצענו במישור הזמן בלבד.
בדוגמה הבאה נדגים כיצד אפשר לפתור
משוואה דיפרנציאלית בעזרת התמרות לפלס. נפנה שוב למעגל שבאיור 15.3:
נתון שברגע t = 0 מתח הקבל הוא אפס.
נמצא ביטוי למתח הקבל כתלות בזמן.
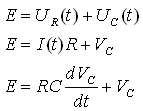
נבצע התמרת לפלס על שני צדי
המשוואה (האות L מבטאת התמרת לפלס על הביטוי בתוך
הסוגריים המצוירות {} )
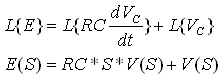
כאשר 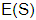 היא התמרות לפלס של
הפונקציות
היא התמרות לפלס של
הפונקציות 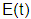 (במקרה זה מדובר בהתמרת
לפלס של קבוע)
(במקרה זה מדובר בהתמרת
לפלס של קבוע)
ו- 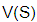 היא התמרת לפלס של המתח
היא התמרת לפלס של המתח 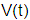
התמרת לפלס של הקבוע E היא 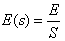 לכן:
לכן:
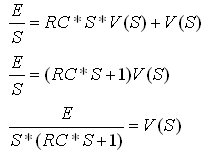
נרשום את השבר בצד שמאל
של המשוואה, כך:
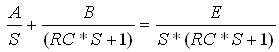
(15.1)
כאשר A, B
הם קבועים. לשם מציאתם נכפיל את שני אגפי המשוואה במכנה המשותף ונקבל:
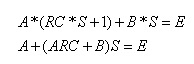
המקדם שמכפיל את S בצד ימין של המשוואה הוא
אפס (אין S) ולכן גם המקדם שמכפיל
את S בצד ימין של המשוואה חייב
להיות אפס. מכאן יוצא ש:
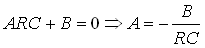
באופן דומה אפשר להגיד שהמקדם החופשי (שאינו מכפיל את S)
בצד ימין של המשוואה הוא E לכן A
= E ומכאן:
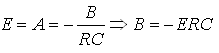
נציב חזרה במשוואה
15.1 ונקבל:
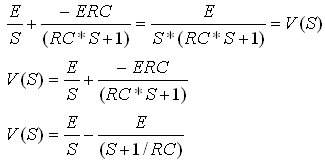
(15.2)
נשתמש בטבלת התמרות לפלס המאפשרת את מציאת התמרת לפלס של פונקציה
התלויה בזמן. אך ידועה הפונקציה במישור לפלס, נוכל לקבל אפוא מן הטבלה את הפונקציה
התלויה בזמן.
לדוגמה, מובאת טבלה חלקית של התמרות לפלס המתאימה לבעיה המוצגת:
בהסתמך על טבלה זאת נוכל
להגיד שהפונקציה הזמנית המתאימה ל- 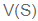 שבמשוואה 15.2 היא:
שבמשוואה 15.2 היא:
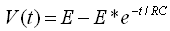
(15.3)
הפונקציה שהתקבלה
(15.3) היא מקרה פרטי של משוואת הדפקים כאשר תנאי ההתחלה הוא אפס.