קורס בתורת החשמל מאת יוסי יאשי

(Transitional phenomena in DC Circuits - first order circuits)

מעגל הניתן לתיאור על ידי משוואה דיפרנציאלית מסדר ראשון ייקרא בשם מעגל מסדר ראשון. משוואה דיפרנציאלית נקראת מסדר ראשון אם הנגזרת הגבוהה ביותר המופיעה במעגל, היא נגזרת ראשונה.

דוגמה למעגל מסדר ראשון הוא מעגל RC טורי המתואר באיור 15.3.

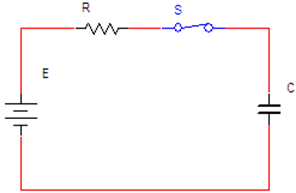
איור 15.3

בתחילת פרק זה (וגם בפרק 7) ראינו כיצד אפשר לרשום משוואה דיפרנציאלית של מעגל חשמלי. בפרק 7 השתמשנו במשוואת הדפקים שהיא פתרון של משוואה דיפרנציאלית מסדר ראשון. בהמשך נראה כיצד אפשר לפתור משוואה דיפרנציאלית מסדר ראשון. יש דרכים אחדות לפתרון משוואה דיפרנציאלית.

פתרון המשוואה הדיפרנציאלית בעזרת המשוואה האופיינית:

נבטא את ההתנגדות השקולה ש"רואה" מקור המתח במישור לפלס – נסמנה באות Z:

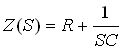
אם נשווה ביטוי זה לאפס נקבל את המשוואה האופיינית של המעגל.

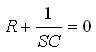
נמצא את שורשי המשוואה האופיינית, כלומר ערכי S המקיימים את איפוס המשוואה.

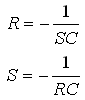
התקבל שורש אחד למשוואה. שימו לב, התוצאה שהתקבלה היא קבוע הזמן, 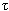שהכרנו כבר בפרק 7.

פתרון המשוואה הדיפרנציאלית כולל שני מרכיבים:

1.     הפתרון ההומוגני (הנקרא גם פתרון דינמי) זהו פתרון המשוואה הדיפרנציאלית כשמשווים אותה לאפס

2.     הפתרון הפרטי (נקרא גם הפתרון הסטטי, או הפתרון המאולץ) פתרון זה תלוי בסוג המקור המחובר למעגל.

לדוגמה: אם המקור הוא מקור מתח ישר, גם הפתרון הפרטי יהיה ערך קבוע כלשהו. אם המקור הוא סינוסואידאלי, גם הפתרון הפרטי יהיה בצורת סינוס.

נרשום את משוואת הזרם הכללית של המעגל המתואר באיור 15.3. משוואה זו מתארת את השתנות הזרם במעגל מרגע סגירת המפסק ועד לרגע שבו הקבל נטען במלואו.

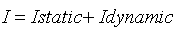
כאשר:

I static -  הזרם במצב המתמיד (לאחר זמן רב)

I dynamic - הזרם במעגל בתקופת המעבר

במצב המתמיד הקבל טעון למלוא המתח ומתנהג כמו נתק ולכן הזרם במעגל שווה אפס.

( I static = 0).

הפתרון ההומוגני, בתקופת המעבר, למעגל מסדר ראשון הוא מן הצורה הזאת:

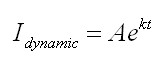
כאשר:

  k - שורש המשוואה האופיינית של המעגל, שאותו מצאנו בתחילת הפתרון.

נציב את ערכו של k ונקבל:

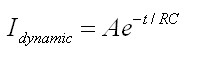
A – מקדם קבוע שניתן לחישוב בעזרת תנאי ההתחלה (מחושב במשוואת הזרם הכללית בלבד)

למשל, עבור t=o הקבל מתנהג כקצר ולכן עצמת הזרם במעגל ניתנת לחישוב:

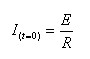
כעת נוכל למצוא את A. נתמקד במשוואת הזרם הכללית הכוללת גם את הזרם הסטטי וגם את הזרם הדינמי.

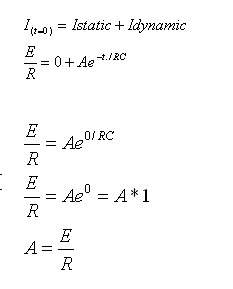
נרשום את משוואת הזרם במעגל:

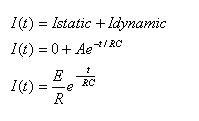
אפשר לראות שהתקבלה משוואה שהיא מקרה פרטי של משוואת הדפקים.

כעת נתבונן במעגל RL טורי בזרם ישר כמתואר באיור 15.4. זוהי דוגמה נוספת  למעגל מסדר ראשון.

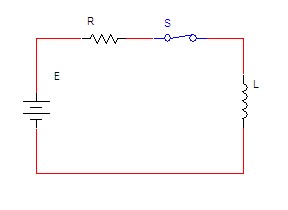
                                                           איור 15.4

גם כאן נבטא את ההתנגדות השקולה ש"רואה" מקור המתח במישור לפלס:

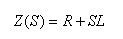
אם נשווה ביטוי זה לאפס נקבל את המשוואה האופיינית של המעגל.

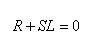
נמצא את שורשי המשוואה האופיינית, כלומר ערכי S המקיימים את איפוס המשוואה.

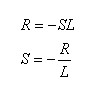
גם כאן התקבל שורש אחד למשוואה.

נרשום את משוואת הזרם של המעגל המתואר באיור 15.4. משוואה זו מתארת את השתנות הזרם במעגל מרגע סגירת המפסק ועד הרגע שבו  הסליל נטען במלואו.

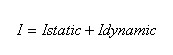
כאשר:

I static – הזרם במצב המתמיד (לאחר זמן רב)

I dynamic – הזרם במעגל בתקופת המעבר

במצב המתמיד הסליל הופך לקצר ולכן הזרם במעגל שווה:

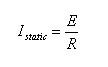
בתקופת המעבר, בעבור מעגל מסדר ראשון משוואת הזרם תירשם כך:

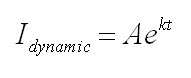
כאשר:

 k– שורש המשוואה האופיינית של המעגל

A – מקדם קבוע שניתן לחישוב בעזרת תנאי ההתחלה.

למשל, עבור t=o הסליל מתנהג כנתק ולכן עצמת הזרם במעגל שווה לאפס.

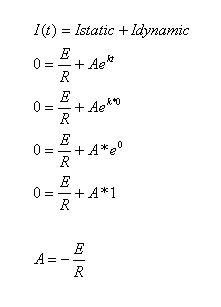
נרשום את משוואת הזרם במעגל:

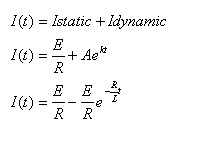
אפשר לראות שהתקבלה משוואת הדפקים, כאשר תנאי ההתחלה הוא אפס.

הערה:

אם אפשר לצמצם בין הקבלים באותו המעגל לקבל אחד שקול, עדיין המעגל נקרא מעגל מסדר ראשון. הטענה הזאת נכונה גם לגבי מעגל הכולל כמה סלילים שאפשר לצמצמם לסליל אחד שקול.

•   הקודם                                                                                                                           
•   המשך