קורס בתורת החשמל מאת יוסי יאשי

(Transitional phenomena analysis in Laplace plane)

בפרקים קודמים נעזרנו במשוואת הדפקים לניתוח תופעות מעבר במעגלי RC ו- RL בזרם ישר. כזכור, משוואת הדפקים מאפשרת לחשב את המתח (או הזרם), ברכיבים שונים של המעגל, כתלות בזמן. שימוש כזה, במשוואת הדפקים, נקרא ניתוח במישור הזמן. יש דרכים נוספות לניתוח תופעות מעבר ברשתות חשמל הן בזרם ישר והן בזרם חילופין: דרך אחת היא ניתוח במישור התדר, כלומר הצגת המתח (או הזרם) ברכיבי המעגל כתלות בתדר של אות הכניסה השנייה ועוד דרך היא הצגת המתח (או הזרם) ברכיבי המעגל במישור  הנקרא מישור לפלס (מישור זה דומה במעט למישור התדר). השימוש במישור לפלס מתאפשר בזכות התמרות לפלס. הלימוד המפורט של התמרות לפלס מחייב שימוש במתמטיקה גבוהה שאינה נכללת בתכנית הלימודים. כאן נציג בקצרה את הכללים שיאפשרו לנו את השימוש במשוואות לפלס בלי להיכנס לעומקה של המתמטיקה הנדרשת.

פתרון רשתות חשמל הכוללות סלילים ו/או קבלים במישור זה הוא בשבילנו, לעתים, כלי מתמטי נוח יותר מפתרון משוואות במישור הזמן או מישור התדר.

כדי להדגים את השימוש במישור לפלס, נציג שתי דוגמאות:  את חוק המתחים של קירכהוף במעגל RL טורי המתואר באיור 15.1 וגם במעגל RC טורי המתואר באיור 15.2  נערוך את הניתוח בשלושה מישורים: מישור זמן, מישור תדר ומישור לפלס.

מעגל RL טורי

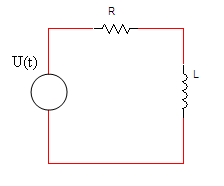
                                                                            איור 15.1

ננצל את המעגל הזה כדי להדגים את המעבר ממישור הזמן וממישור התדר למישור לפלס. כל זאת כדי לפתור את זרמי המעגל. שימו לב, אנו נשתמש בחוק המתחים של קירכהוף, אך בסופו של דבר נחשב את זרמי המעגל.

על פי חוק המתחים של קירכהוף אפשר לרשום:

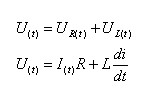
נחלק את המשוואה ב- R לקבלת משוואה דיפרנציאלית לזרם

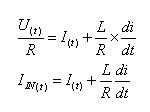
אם זרם הכניסה הוא זרם קבוע  או מדרגה, פתרון המשוואה הדיפרנציאלית הוא משוואת הדפקים לזרם.

הערה: כדי לקבל פתרון יחיד למשוואה דיפרנציאלית מסדר ראשון, חייב להיות תנאי התחלה אחד ידוע.

אפשר להציג את חוק המתחים של קירכהוף – גם במישור התדר (w):

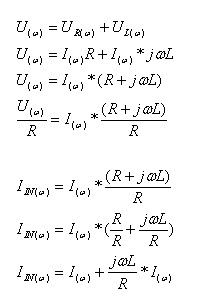
המעבר מחוק המתחים של קירכהוף במישור התדר לחוק המתחים במישור לפלס (S) הוא מידי. 

כל שעלינו לעשות הוא להחליף את 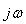 ב- S  ואז נקבל:

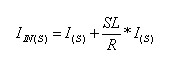
אם נתבונן היטב במשוואה במישור לפלס ונשווה אותה למשוואה הדיפרנציאלית במישור הזמן, ודאי נראה שפעולת הגזירה של הזרם, במישור הזמן, שקולה להכפלת הזרם ב- S, במישור לפלס.

הערה: החלפת הנגזרת בהכפלה ב- S מותרת רק אם תנאי ההתחלה הוא אפס. שאם לא כן, יש להחליף את הנגזרת ב-  S*I(S) – I(0)

כאשר: I(0) הוא ערך הזרם ברגע אפס.

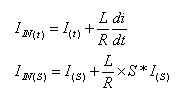
אכן, זה אחד היתרונות הבולטים של השימוש במישור לפלס.

הפתרון שנקבל במקרה זה הוא הפונקציה I_(S), שהיא התמרת לפלס של הפונקציה I_(t). בעזרת טבלאות מתאימות אפשר לעבור מפונקציה במישור הזמן לפונקציה במישור לפלס.

מעגל RC טורי

בדומה לניתוח שנעשה לגבי מעגל RL, גם כאן נראה כיצד אפשר לפתור את משוואות המתחים במעגל בשלושה מישורים.

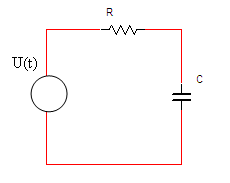
                                                              איור 15.2

חוק המתחים של קירכהוף – במישור הזמן (t):

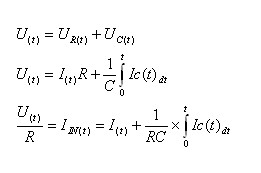
חוק המתחים של קירכהוף – מישור התדר (w):

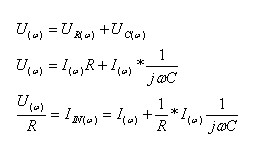
המעבר מחוק המתחים של קירכהוף במישור התדר לחוק המתחים במישור לפלס (S):הוא מידי. כל מה שעלינו לעשות הוא להחליף את 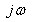ב- S ואז נקבל:

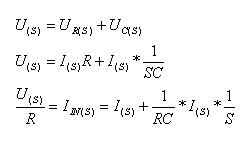
אם נתבונן היטב במשוואה במישור לפלס ונשווה אותה למשוואה הדיפרנציאלית במישור הזמן, נראה שפעולת האינטגרציה של הזרם, במישור הזמן, שקולה לחלוקת הזרם ב- S, במישור לפלס. זהו יתרון נוסף של השימוש במישור לפלס.

הפתרון שנקבל במקרה זה הוא הפונקציה I_(S), שהיא התמרת לפלס של הפונקציה I_(t).

הערה: החלפת האינטגרל בחלוקה ב- S מותרת רק אם תנאי ההתחלה הוא אפס. שאם לא כן, יש להחליף את

הנגזרת ב-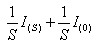 

כאשר: I(0) הוא ערך הזרם ברגע אפס.

בעזרת טבלאות מתאימות אפשר לעבור מפונקציה במישור הזמן לפונקציה במישור לפלס.

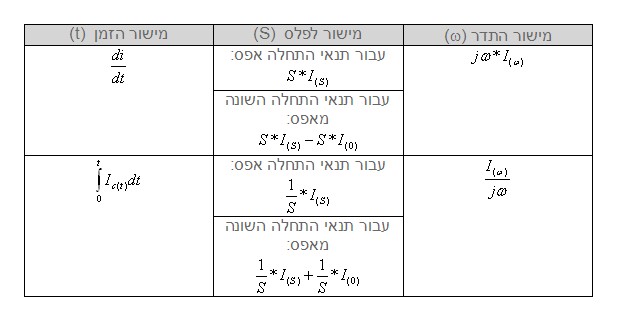
בטבלה הבאה נרכז את ההמרות הבסיסיות בין המישורים השונים שבהן נעזרנו עד כה:

•   הקודם                                                                                                                            
•  המשך