קורס בתורת החשמל מאת יוסי יאשי

(Symmetric square signal decomposition using Fourier series)

נתון האות המחזורי שבאיור 14.4.

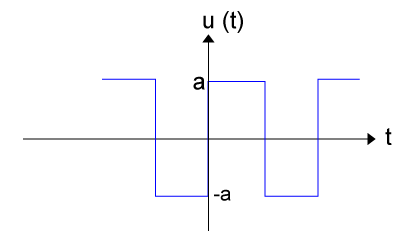
איור 14.4

האות הריבועי שמתואר באיור 14.4 סימטרי גם בעבור ציר ה- X וגם בעבור מערכת הצירים. על כן פירוק האות על פי פורייה צריך לכלול הרמוניות אי זוגיות ואך ורק סינוסים.

רישום הטור בצורה כללית:

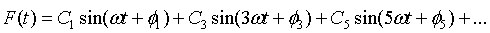
פירוק אות מחזורי ריבועי מן הצורה שמתוארת באיור 14.4 יהיה כך (פיתוח הטור חורג ממסגרת הנושא הנלמד כאן והוא נלמד במסגרת קורס אחר העוסק בנושא טורי פורייה):

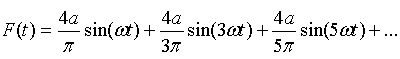
הערות:

1. 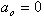 כי ערכו הממוצע של האות שווה לאפס, שאם לא כן המקדם הזה היה מופיע לפני כל הטור.

2. 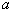 מבטא את ערכו המרבי של האות.

באיור 14.5 מתואר האות המחזורי הריבועי ופירוקו להרמוניות בהתאם לטור פורייה.

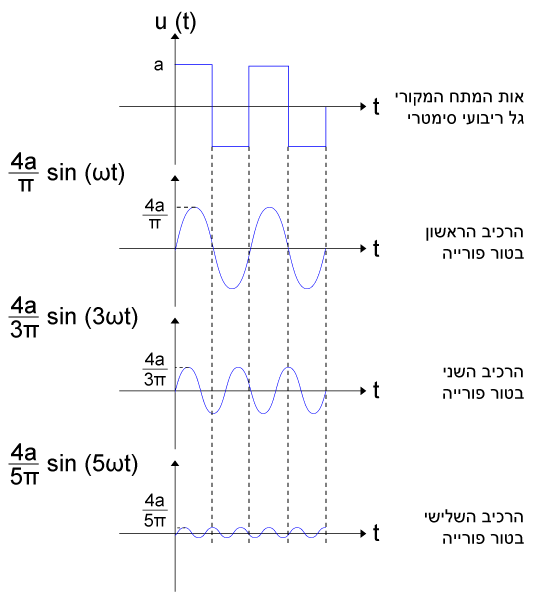
איור 14.5

הערה:

ככל שההרמוניה גבוהה יותר, כן משרעתה נמוכה יותר. בעבור n גבוה אפשר להזניח את המשרעת כיוון שהיא נמוכה מאוד.

כעת נבצע תהליך הפוך של חיבור רכיבי הטור לקבלת האות המקורי. באיור 14.6 מתואר אות לאחר חיבור הרמוניה הראשונה והשנייה.

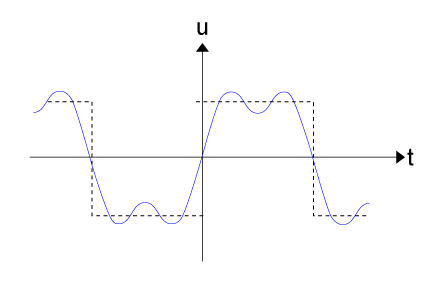
איור 14.6

באיור 14.7 מתואר אות לאחר חיבור הרמוניה ראשונה, שנייה ושלישית.

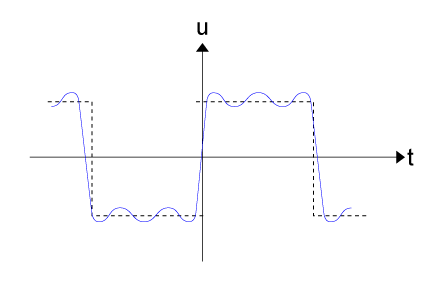
איור 14.7

אפשר לראות שאם נחבר את כל ההרמונית נגיע לאות המקורי שהוא גל ריבועי.

הערה: אפשר לראות מאיור 14.7 שדי בסכום שלוש ההרמוניות הראשונות בלבד, כדי שנקבל צורה דומה מאוד  לצורת האות המקורית (גל ריבועי). לכן, כשמבצעים סינתזה של ההרמוניות לצורך קבלת האות המקורי אפשר להסתפק בחמש ההרמוניות הראשונות.                                   

לחצו כאן לפירוק אות ריבועי להרמוניות גבוהות מאוד

•   הקודם                                                                                                                             
• המשך