קורס בתורת החשמל מאת יוסי יאשי

(Parallel magnetic circuits)

יש התקנים אלקטרומגנטים הבנויים מכמה קורות ולאו דווקא מחומרים המהווים חוג סגור אחד כפי שראינו בתת הפרקים 13.1 ו- 13.2. דוגמאות להתקנים כאלה יכולות להיות סוגים שונים של שנאים חד-מופעיים ותלת- מופעיים.

המעגל המקבילי המגנטי הקלאסי מתואר באיור 13.37 - מעגל הבנוי משלוש קורות המהוות שלושה מסלולים מגנטים:

 המסלול המגנטי השמאלי bafe

הקורה המרכזית be

המסלול  המגנטי הימני bcde

 בסך הכול שלושה מיאונים במעגל המגנטי - כל מיאון מצוי בענף מקבילי אחר

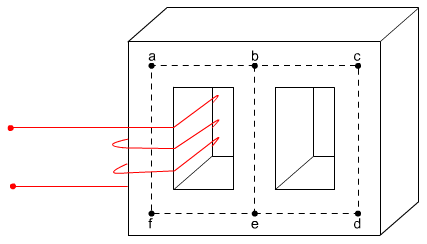
איור 13.37

כדי להבין כיצד עובר השטף המגנטי בליבה כולה מומלץ לסרטט מעגל חשמלי האנלוגי למעגל המגנטי. במעגל המתואר באיור 13.38 במעגל יש שלוש התנגדויות מגנטיות המחוברות במקביל. הכמ"מ מחובר בטור להתנגדות השמאלית.

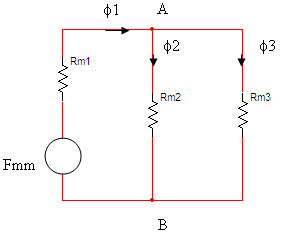
איור 13.38  

Rm₁ = Rbafe;     Rm₂ = Rbe;      Rm₃ = Rbcde

אמנם קיימים שלושה ענפים מקביליים, אך אפשר לראות שהמעגל שהתקבל הנו מעגל מעורב. במעגל זה מתקיימות התכונות האלה:

חישוב מיאון שקול (ש"רואה" הכמ"מ)

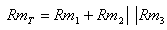
חישוב השטף הכללי (בתוך הסליל - "מסופק מהכמ"מ)

ניעזר ב"חוק אוהם המגנטי":

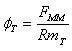
שימוש ב"חוק הזרמים המגנטי" של קירכהוף:

נזכיר שבאנלוגיית המעגל החשמלי למעגל המגנטי השטף המגנטי מהווה את הזרם במעגל.

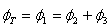
שימוש ב"חוק המתחים המגנטי" של קירכהוף:

נזכיר שבאנלוגיית המעגל החשמלי למעגל המגנטי מכפלת המיאון בשטף (או עצמת השדה באורך המסלול המגנטי) מהווה את מפל המתח.

נרשום את משוואות "המתחים המגנטים" בהתאם למספר החוגים במעגל:

בעבור החוג השמאלי:

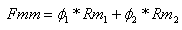
או בצורה אחרת:

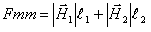
בעבור החוג הגדול (ללא האמצע):

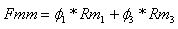
או בצורה אחרת:

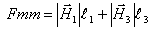
בעבור החוג הימני:

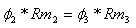
או בצורה אחרת:

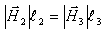
הערות:

1.     אפשר להיעזר גם בכלל מחלק המתח וכלל מחלק הזרם.

2.     אם קיים כמ"מ נוסף על גבי קורה אחרת, מתקבל מעגל חשמלי שאותו אפשר לפתור באמצעות משפטי רשת או שיטות לפתרון רשתות.

3.     חריץ האוויר במעגלים האלה מהווה התנגדות נוספת במעגל. מיאון האוויר יהיה בטור למיאון הענף שבו הוא מצוי.

•   הקודם                                                                                                                            
•  המשך