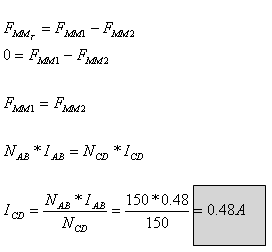קורס בתורת החשמל מאת יוסי יאשי

תרגיל דוגמה 1

באיור 13.4 נתונה ליבת ברזל בעל חדירות מגנטית יחסית של 1150. הליבה בעלת שטח חתך אחיד של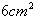 

ואורך המסלול הממוצע של המעגל המגנטי 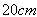. על ליבה זו מלפפים סליל בעל 200 כריכות ומחברים אותו דרך מפסק למקור מתח ישר.

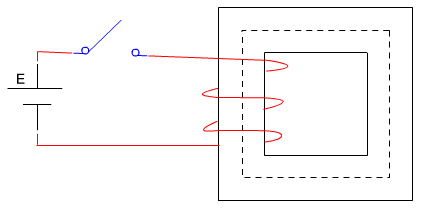
איור 13.4

חשבו את:

א. המיאון המגנטי של הליבה;

ב. עם סגירת המפסק עובר בסליל זרם של 2A. חשבו את השטף המגנטי בליבת הברזל וקבעו את מגמתו;

ג. מהי עצמת השדה המגנטי H בליבה?

פתרון תרגיל דוגמה 1

במעגלים מגנטיים מומלץ לסרטט את המעגל החשמלי האנלוגי למעגל המגנטי, לפני תחילת הפתרון - איור 13.5

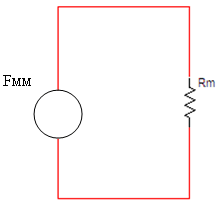
13.5

נסרטט שוב את המעגל החשמלי האנלוגי למעגל המגנטי, אך הפעם עם קוטביות הכמ"מ - איור 13.7.

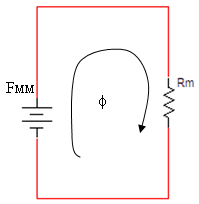
איור 13.7 

א. נחשב את המיאון במעגל המגנטי:

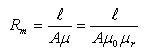
יש לשים לב ליחידות של הגדלים, בעת החישוב. למשל:

נתון שאורך המסלול הממוצע של המעגל המגנטי 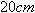. עלינו לבטא את ה- 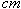ב- m על ידי חלוקה ב- 100 או הכפלה ב-.

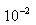נתון שהליבה בעלת שטח חתך אחיד של 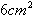. עלינו להפוך את ה- 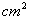ל-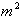 על ידי חלוקה ב- 10000 או הכפלה ב -.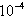

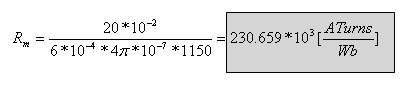
ב. ניעזר ב"חוק אוהם המגנטי" לקביעת עצמת השטף במעגל:

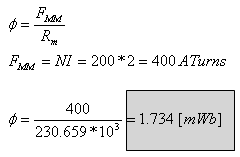
מגמת השטף המגנטי כאמור היא עם כיוון השעון (בהתאם לכלל יד ימין).

ג. עצמת השדה המגנטי בתוך הסליל תלויה בכמ"מ ובאורך הסליל, עצמה זו שווה בכל ליבת הברזל. אבל מכיוון שאיננו יודעים את אורך הסליל, יהיה עלינו לחשב את עצמת השדה המגנטי באמצעות החלחלות המגנטית וצפיפות השטף המגנטי. 

נחשב את ההשראה המגנטית (צפיפות השטף המגנטי) בעזרת השטף המגנטי בליבה:

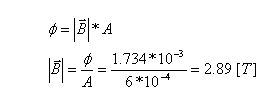
כעת אפשר לחשב את עצמת השדה המגנטי בתוך הסליל ובליבה בכלל:

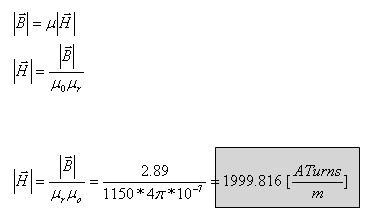
אפשר גם לחשב את עוצמת השדה המגנטי בליבה בדרך נוספת:

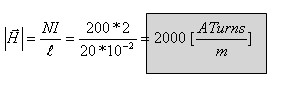
תרגיל דוגמה 2

סליל בעל 500 כריכות מלופף על חומר פרומגנטי בעל חדירות יחסית 950 שצורתו גלילית וקוטרו 1 ס"מ . את החומר כופפו לצורת טבעת בעלת היקף של 60 ס"מ. הטבעת נכנסת לרוויה מגנטית כאשר צפיפות השטף המגנטי בליבה מגיע ל- 1.2T.

חשבו את:

א. מיאון החומר הפרומגנטי;

ב. מה הזרם המרבי שיכול לעבור בסליל בלי שהטבעת תהיה ברוויה מגנטית?

פתרון תרגיל דוגמה 2

נרכז את נתוני השאלה:

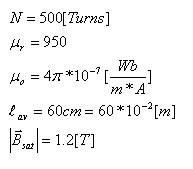
קוטר הטבעת 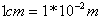 לכן אפשר לחשב את שטח החתך של הטבעת:

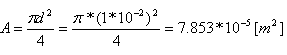
א. חישוב ההתנגדות המגנטית (מיאון):

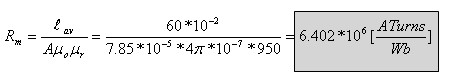
ב. נסרטט מעגל חשמלי אנלוגי למעגל המגנטי המתואר בשאלה- איור 13.8. 

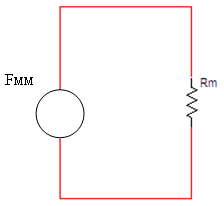
איור 13.8

הטבעת נכנסת לרוויה מגנטית בעבור 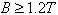 . נמצא מהו השטף המגנטי בעבור השראה מגנטית של 1.2 טסלה.

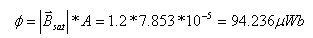
נחשב כעת מהו גודל הכמ"מ שיוצר שטף זה בליבה (ניעזר באיור 13.8), ולאחר מכן נוכל לקבוע את עצמת הזרם המרבית שיכולה לעבור בסליל  כדי שהמעגל המגנטי לא ייכנס לרוויה.

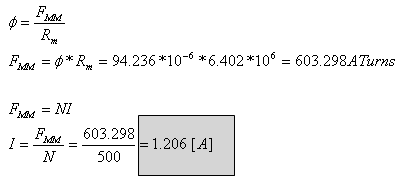
חשוב לציין כי בתחום הרוויה המגנטית, הגדלת הזרם במוליך משפיעה על עצמת השדה המגנטי ומאחר שבתחום זה החלחלות המגנטית משתנה, גם המיאון של המעגל המגנטי משתנה! ברוויה מגנטית השטף המגנטי וצפיפות השטף המגנטי קבועים ואינם תלויים בעצמת השדה המגנטי.

תרגיל דוגמה 3

המיאון המגנטי של המעגל המגנטי המתואר באיור 13.9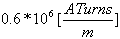 

הסליל שמלופף על הליבה עשוי נחושת (התנגדות סגולית 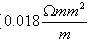 ) ואורכו 280 ס"מ והוא בעל שטח חתך של 0.5 ממ"ר.

ידוע שמספר הכריכות 300. 

ממדי הליבה רשומים באיור 13.9

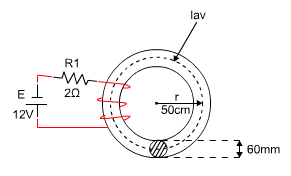
איור 13.9

חשבו את:

א. השטף המגנטי בליבה - קבעו את מגמתו;

ב. צפיפות השטף המגנטי בליבה;

ג. החלחלות היחסית של החומר הפרומגנטי המתואר בשאלה;

ד. ההשראות העצמית של הסליל.

פתרון תרגיל דוגמה 3

בתרגיל זה, מקור המתח מחובר בטור עם נגד של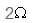לסליל שאנו יכולים לחשב את התנגדותו החשמלית. כלומר עלינו להתייחס תחילה למעגל החשמלי (האמיתי - לא לזה האנלוגי למעגל המגנטי) ולחשב בו את הזרם.

את ההתנגדות החשמלית של הסליל אפשר לחשב בעזרת הנוסחה לחישוב התנגדות חשמלית - השפעת סוג המוליך ומידותיו הגאומטריות של המוליך על התנגדותו:

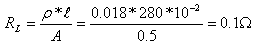
יש לשים לב שבנוסחה זו יחידות שטח החתך של המוליך (לא של הליבה) הן בממ"ר.

נסרטט את המעגל החשמלי ונחשב בו את הזרם - איור 13.10

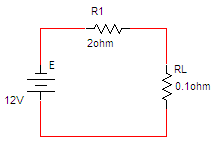
איור 13.10

א. נסרטט מעגל חשמלי אנלוגי למעגל המגנטי המתואר בשאלה - איור 13.11

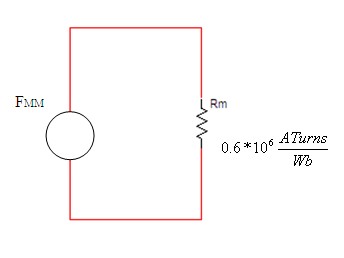
איור 13.11

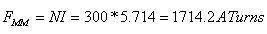
על פי "חוק אוהם המגנטי":

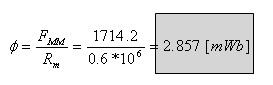
מגמת השטף המגנטי כפי שמתואר באיור 13.12 היא נגד כיוון השעון!

ב. נחשב את צפיפות השטף המגנטי בליבה:

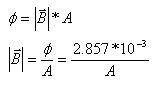
באיור 13.19 הנתון בשאלה אפשר לראות שלטבעת קוטר של 60 מ"מ. לכן אפשר לחשב את שטח החתך של הטבעת (היחידות הדרושות הן במ"ר):

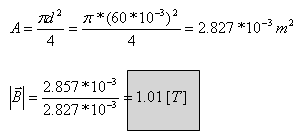
ג. לצורך חישוב החדירות היחסית של הליבה ניעזר בנוסחה לחישוב המיאון:

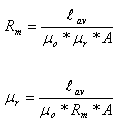
את ממוצע אורך המסלול המגנטי אפשר לחשב כפי שמחשבים היקף של מעגל, ראו איור 13.9

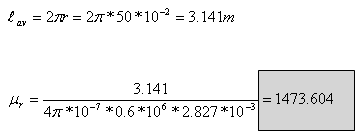
הערה: חישוב החדירות המגנטית היחסית מתייחס לאזור הלינארי של עקומת החשל בחומר הפרומגנטי - שם בקירוב טוב החדירות קבועה ואינה משתנה.

ד. חישוב ההשראות העצמית של סליל כפי שהובא בפרק 9:

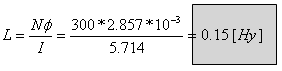
את ההשראות העצמית במעגלים מגנטיים אפשר לחשב גם כך:

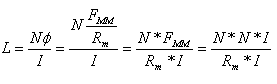
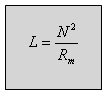
(13.4)

כאשר:

L - השראות עצמית של הסליל  [Hy]

N - מספר הכריכות

Rm - מיאון המעגל המגנטי 

חשבו את ההשראות העצמית גם בעזרת נוסחה 13.4 והיווכחו בתוצאה.

תרגיל דוגמה 4

על ליבה פרומגנטית 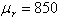 מלפפים שני סלילים, כמתואר באיור 13.13. אורכו הממוצע של המסלול המגנטי 6 ס"מ ושטח החתך של הליבה 80 ממ"ר. מספר הליפופים זהה בכל אחד מן הסלילים.

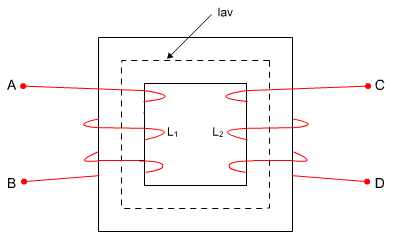
איור 13.13

בין ההדקים AB מחברים מקור מתח ישר של 4 וולט (קוטביות חיובית כלפי נקודה B), ואילו בין הדקים CD מחברים נגד שערכו .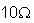

עצמת השדה המגנטית בליבה במצב זה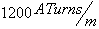 

ההשראות העצמית של הסליל L1 הנה 32mH.

חשבו את:

א. השטף המגנטי בליבה ואת מגמתו;

ב. הספק הנמסר על ידי מקור המתח שמחובר בין ההדקים AB;

ג. המתח מושרה בין הדקי הסליל CD;

ד. מנתקים את הנגד מן המעגל ובמקומו מחברים מקור מתח ישר. מה צריכה להיות קוטביות המקור ואיזה זרם הוא צריך לספק כדי שצפיפות השטף המגנטי בליבה תתאפס?

פתרון תרגיל דוגמה 4

נסרטט תחילה את המעגל החשמלי האנלוגי למעגל המגנטי. בסליל AB מחברים מקור מתח ולכן מבחינה מגנטית נוצר כמ"מ (כוח אלקטרו מניע). אך בסליל CD מחובר נגד, כך שסליל זה מבחינה מגנטית אינו משפיע על המעגל המגנטי (הכמ"מ בו שווה לאפס).

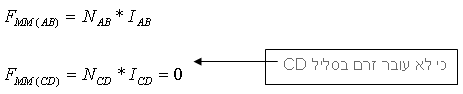
הזרם בסליל AB נכנס מהדק B לתוך הסליל ויוצא לכיוון הדק A (מקור המתח מחובר עם קוטביות חיובית כלפי הדק B). לכן על פי כלל יד ימין נקבל שקוטביות הכמ"מ היא כלפי מטה.

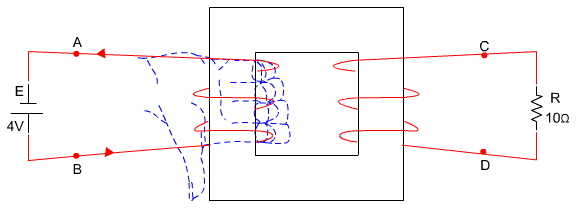
איור 13.14

באיור 13.15 נסרטט את המעגל החשמלי האנלוגי למעגל המגנטי ונרכז את נתוני השאלה:

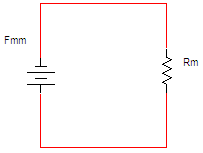
איור 13.15

א. נתון:

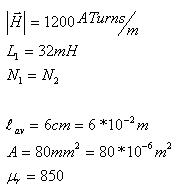
נחשב את צפיפות השטף המגנטי בליבה:

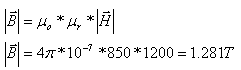
בעזרת שטח החתך של הליבה אפשר לחשב את השטף המגנטי בליבה:          

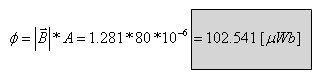
מגמת השטף המגנטי כפי שאפשר לראות באיור 13.15 היא נגד כיוון השעון.

ב. הספק מקור המתח הישר:

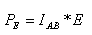
כדי לחשב את ההספק שנמסר על ידי מקור המתח עלינו למצוא את הזרם שעובר בסליל AB. את עצמת הזרם בסליל AB נחשב בעזרת הכמ"מ של אותו הסליל.

ניעזר בנוסחה לחישוב השראות עצמית

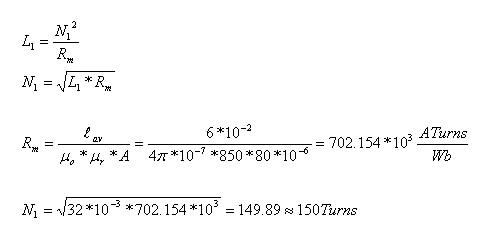
כפי שלמדנו בפרק 8, את עצמת השדה המגנטי בתוך הסליל (שווה ערך גם לעצמת השדה המגנטי בליבה) אפשר לבטא כך (וזה גם היישום של חוק אמפר בטורואיד):

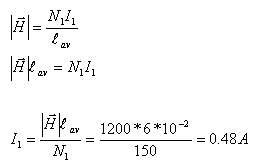
כעת אפשר לחשב את ההספק שנמסר על ידי מקור המתח E:

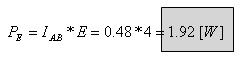
ג. מתח מושרה בסליל מתקיים אם קיים שינוי של שטף מגנטי בסליל. חיבור מקור מתח ישר בין הדקי הסליל AB יוצר שטף מגנטי קבוע בליבה שעובר גם בסליל CD. אך מאחר ששטף זה קבוע ואינו משתנה, לא קיים מתח מושרה בסליל CD.

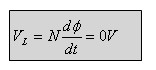
ד. עם ניתוק הנגד וחיבור מקור מתח ישר במקומו בין ההדקים CD, מופיע כמ"מ נוסף במעגל. כדי שצפיפות השטף המגנטי B תתאפס, עלינו לדרוש שהשטף המגנטי בליבה 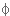 יתאפס.

חיבור אנטי טורי בין שני הכממי"ם יגרום לכך שהכמ"מ השקול יהיה שווה לאפס ובכך גם השטף המגנטי יתאפס. על כן, נדרוש מן הכמ"מ של סליל CD להיות שווה לכמ"מ של סליל AB ומנוגד לו בקוטביות.

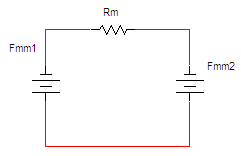
איור 13.16

•   הקודם                                                                                                                             
• המשך