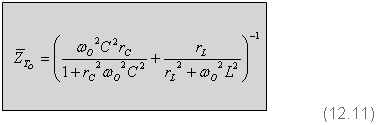(Two-branch parallel resonant circuit in AC)
בתת הפרק מעגל תהודה מקבילי בזרם חילופין, ההתייחסות הייתה אך ורק
לקבל ולסליל אידאליים (ללא התנגדות פנימית r). חיבור
מקבילי בין סליל ובין קבל שלפחות אחד מהם הוא רכיב מעשי (עם התנגדות פנימית),
יוצרת מעגל מקבילי דו-ענפי בעל תכונות השונות מן החיבור המקבילי הטהור.
נתבונן במעגל שבאיור 12.30 - מעגל דו-ענפי מקבילי המכיל קבל וסליל
מעשיים.
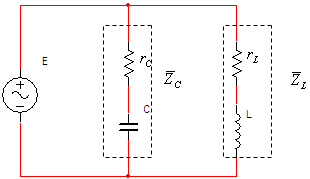
איור 12.30
יש סיכוי שהמעגל שבאיור 12.30 יהיה במצב תהודה, כי מתקיים בו התנאי
הראשוני לתהודה "לפחות
קבל אחד וסליל אחד". כשהמעגל יהיה בתהודה, הפרש המופע בין
מתח המקור לזרם המקור יהיה שווה אפס. במעגל
דו-ענפי, תהודה תתקיים לא בהכרח כשהיגב הקבל והיגב הסליל שווים זה לזה.
התנאי הכללי לתהודה במעגל בזרם חילופין שיש בו לפחות קבל אחד וסליל
אחד הוא שעכבת המעגל תרגיש התנגדות ממשית בלבד (החלק הדמיוני מתאפס).
נבדוק מהם התנאים שמביאים את המעגל הדו-ענפי הזה למצב תהודה, על פי
השלבים האלה:
1. יש לבטא את עכבת המעגל כתלות בכל התנגדויות המעגל;
2. רישום העכבה הכללית
חייב להיות מן הצורה 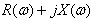
3. יש להשוות את החלק
הדמיוני לאפס ולמצוא את התדר שמביא לאיפוס החלק הזה. תדר זה, אם קיים, הוא תדר
התהודה של המעגל.
נמצא ביטוי לעכבת המעגל הדו-ענפי המתואר באיור 12.30:
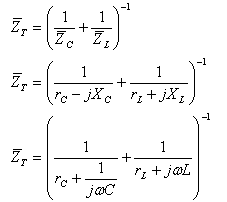
נכפול מונה ומכנה של הביטוי
השמאלי בתוך הסוגריים ב-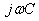 כדי לבטל את השבר:
כדי לבטל את השבר:
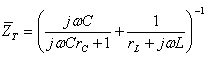
נכפול גם את המונה וגם את המכנה של כל ביטוי בתוך הסוגריים, בצמוד
של המכנה שלו, כדי לקבל במכנה מספר ממשי:
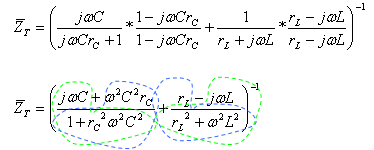
כל ביטוי בתוך הסוגריים נציג כשני ביטויים (ממשי - בכחול ודמיוני -
בירוק):
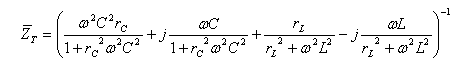
נציג את העכבה השקולה מן
הצורה 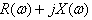
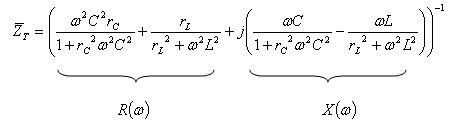
כדי שהמעגל יהיה בתהודה
צריך להתקיים התנאי 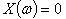
יש לשים לב שמעתה התדר
הזוויתי יירשם כתהודתי 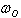
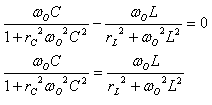
לצורך צמצום ראשוני נכפול
את המשוואה ב-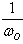
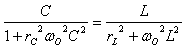
נבצע כפל בהצלבה:
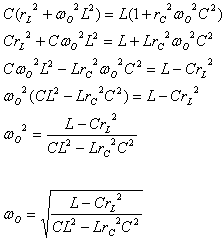
באמצעות הביטוי הזה אפשר לחשב את תדר התהודה הזוויתי בעבור מעגל
דו-ענפי מקבילי כמתואר באיור 12.30.
נבצע עוד כמה פעולות מתמטיות על ביטוי מתמטי זה כדי ליצור נוסחה
כללית למעגל דו-ענפי מקבילי.
נחלק מונה ומכנה בתוך השורש ב- C:
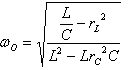
נוציא מתוך המכנה LC מחוץ לסוגריים ונקבל:
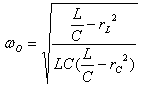
נרשום ביטוי זה בצורה אחרת ונקבל את הנוסחה הכללית למציאת תדר
התהודה הזוויתי במעגל דו-ענפי מקבילי (12.9).
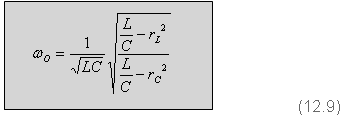
יש הנוהגים לרשום נוסחה
12.9 באמצעות "ההתנגדות האופיינית" RO
(12.10)
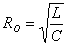
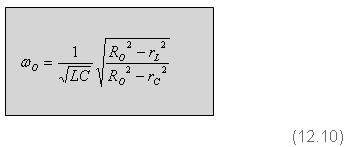
כאשר:
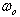
-
תדירות זוויתית תהודתית 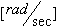
- Lהשראות המשרן [Hy]
C - קיבול הקבל [F]
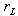 - התנגדות פנימית של המשרן
- התנגדות פנימית של המשרן 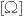
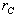
-
התנגדות פנימית של הקבל 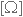
Ro - התנגדות אופיינית (התכנון)
של המעגל. התנגדות שאינה תלויה בתדר. 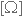
בעזרת נוסחאות 12.9 ו- 12.10 אפשר להסיק כמה דברים:
1.
תהודה אינה יכולה
להתקיים ללא קבל אחד וסליל אחד לפחות.
2. אם הקבל והסליל אידאליים 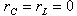 אנו מקבלים את הנוסחה
לחישוב תדר תהודה זוויתי בעבור מעגל מקבילי טהור.
אנו מקבלים את הנוסחה
לחישוב תדר תהודה זוויתי בעבור מעגל מקבילי טהור.
3. אם בתוך השורש מתקבל
ערך שלילי, משמעות הדבר שמתקבל תדר מרוכב. כלומר במצב זה המעגל אינו יכול להיכנס
לעולם לתהודה. רכיבי המעגל קובעים את תדר התהודה וקובעים אם בכלל יכולה להיות
תהודה.
4. בנוסחאות האלה אפשר להשתמש
גם במקרים פרטיים של סליל אידאלי וקבל מעשי או סליל מעשי וקבל אידאלי.
5. חיבור נגד נוסף במקביל
למקור המתח אינו משפיע על התהודה של המעגל, אלא רק על עכבת המעגל.
6. בעבור התנאי 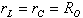 מתקיים שבעבור
כל
מתקיים שבעבור
כל 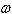 המעגל מצוי
בתהודה.
המעגל מצוי
בתהודה.
7. בעבור
התנאי 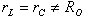 חישוב תדר
התהודה זהה למעגל המקבילי הטהור ולכן במצב זה היגב הסליל שווה להיגב הקבל.
חישוב תדר
התהודה זהה למעגל המקבילי הטהור ולכן במצב זה היגב הסליל שווה להיגב הקבל.
את חישוב עכבת המעגל במצב תהודה בעבור המעגל שבאיור 12.30 אפשר
לבצע בצורה מקוצרת (12.11) - החלק הממשי בפיתוח הנוסחה 12.9, לאחר ביטול החלק
הדמיוני והשוואתו לאפס כתנאי לתהודה.