(Parallel resonance characteristics)
במעגל RLC מקבילי, בדומה למעגל RLC טורי, כשהיגב הסליל שווה להיגב הקבל המעגל מצוי בתהודה. אף על פי
כן יש הבדלים במאפייני התהודה המקבילית לעומת התהודה הטורית.
עכבת המעגל בתהודה
חישוב עכבת המעגל עבור המעגל המקבילי שמתואר באיור 12.23:
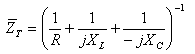
בתהודה היגב הקבל שווה להיגב הסליל:
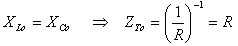
מכאן מתקבל שעכבת המעגל בתהודה שווה לנגד R:
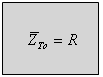
כלומר בתהודה מקור האנרגיה במעגל "רואה" אך ורק את
ההתנגדות הטהורה. או במילים אחרות, עכבת המעגל שווה להתנגדות הנגד.
בשונה מתהודה טורית, עכבת המעגל במצב של תהודה היא מרבית. בכל תדר אחר סביב לתדר התהודה יש
תוספת היגב שקול במקביל לנגד, דבר המקטין את גודל העכבה.
אפשר לתאר את השתנות העכבה כתלות בתדר באמצעות איור 12.24.
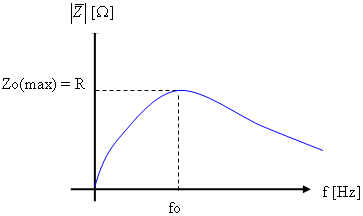
איור 12.24
הזרם בתהודה
חישוב הזרם במעגל יהיה על פי חוק אום:
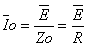
ואם ידוע שבתהודה העכבה מרבית,
משמע שהזרם מזערי
(יחס הפוך).
את השתנות הזרם במעגל כתלות בתדר המקור אפשר לתאר באמצעות איור
12.25:
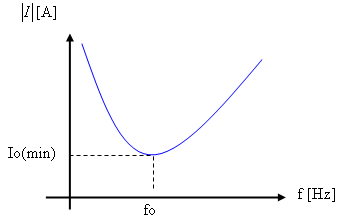
איור 12.25
הסבר לאופיין:
האופיין הזה הפוך לאופיין העכבה המתואר באיור 12.24 - יחס הפוך.
בתדר תהודה עכבת כשהמעגל מרבית, מתקבל זרם מזערי. בתדר אפס ובתדר אינסופי כשעכבת
המעגל שווה אפס, מתקבל זרם השואף לאינסוף.
פאזורי הזרמים בתהודה
על פי חוק הזרמים של קירכהוף:
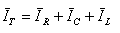
בתהודה, כאמור, היגב הקבל שווה להיגב הסליל ומאחר שהמתח במקביל
שווה, גם הזרם דרך הקבל שווה בגודלו
לזרם דרך הסליל (קיים היפוך מופע של 180°). כלומר הזרם הכולל דרך
הקבל והסליל יחד שווה לאפס, הקבל והסליל בתהודה טורית מתנהגים כמו נתק. לכן אפשר לומר שבתהודה
מקבילית, הקרויה גם
תהודת זרמים, זרם המקור שווה לזרם דרך הנגד R.
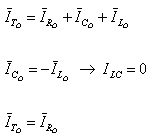
באיור 12.26 נתאר את פאזורי
הזרם במעגל:
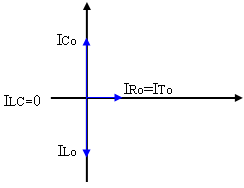
איור 12.26
זווית המופע בתהודה
זווית המופע במעגל מוגדרת כהפרש המופע בין המתח לזרם הכולל במעגל.
זווית זו מתארת את זווית העכבה. אם ידוע שבתהודה עכבת המעגל שווה להתנגדות הנגד,
הרי שזווית המופע היא אפס.
זו הסיבה לכך שבתהודה אין הפרש מופע בין המתח לזרם במעגל.
את השתנות המופע במעגל, כתלות בתדר המקור, אפשר לתאר באמצעות איור
12.27.
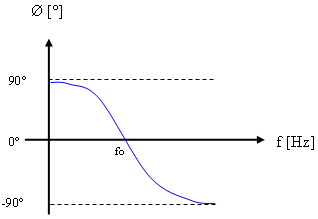
איור 12.27
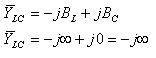
נוסיף את מוליכות הנגד לחישוב מתירות המעגל כולה:
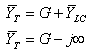
גודל המתירות הכללית תשאף גם כן לאינסוף והיא תהיה בעלת זווית של º90-. לכן עכבת המעגל בתדר אפס תהיה שווה לאפס
בזווית של º90+.
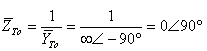
ככל שנגדיל את תדר המקור הזווית תקטן לכיוון האפס, ואילו גודלה של
עכבת המעגל תעלה. בתדר התהודה גודל עכבת המעגל תהיה שווה לנגד R
וזווית המופע תהיה אפס. בתדרים גדולים מתדר התהודה, זווית העכבה הופכת להיות
שלילית - בתדר גבוה מאוד (אינסופי) זווית זו שווה למינוס 90 מעלות.
חישוב תדר התהודה
בדומה לתהודה במעגל הטורי, גם במעגל המקבילי תהודה מתקבלת
כשההיגבים של הקבל והסליל שווים. לכן חישוב תדר התהודה במעגל המקבילי יהיה זהה
לחישובו במעגל הטורי כפי שראינו בנוסחה 12.1 (תדר תהודה טורי).
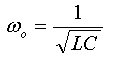
ידוע הקשר שבין תדירות
זוויתית ובין תדר: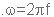 לכן:
לכן:
חישוב תדר התהודה במעגל מקבילי:
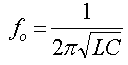
כאשר:
fo- תדר תהודה מקבילי [Hz]
L- גודל המשרן [Hy]
-C גודל הקבל [f]
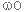 תדירות זוויתית תהודתית-[rad/sec]
תדירות זוויתית תהודתית-[rad/sec]
חישוב רוחב הסרט וגורם הטיב במעגל מקבילי
את גורם האיכות (הטיב) מחשבים בצורה הפוכה מן המעגל הטורי כמתואר
בנוסחה 12.8.
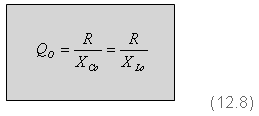
כלומר גורם הטיב בתהודה מקבילית מבטא את היחס בין ההתנגדות האוהמית
של המעגל לבין ההתנגדות ההיגבית.
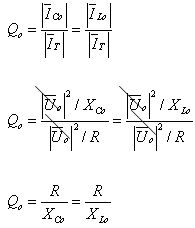
גישה אחרת היא לתאר את גורם הטיב כיחס הזרמים שבין הזרם דרך הרכיב
היגבי לבין זרם המקור - שיעור עליית הזרם התהודתית.
במצב של תהודה מתקיים שוויון זרמים בין הרכיבים ההיגביים:
הערה:
הנגד הנו הרכיב שקובע באופן ישיר את גורם הטיב במעגל. ככל שהתנגדות
הנגד תהיה גדולה יותר, כן גם גורם הטיב יהיה גדול יותר.
חישוב רוחב הסרט זהה לתהודה הטורית כפי שראינו בנוסחה (12.7):
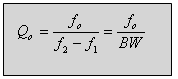
כאשר:
BW- רוחב סרט (פס)
[Hz]
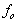
-
תדר התהודה [Hz]
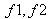 -תדרי מחצית ההספק [Hz]
-תדרי מחצית ההספק [Hz]