קורס בתורת החשמל מאת יוסי יאשי

(Series resonance characteristics)

עכבת המעגל בתהודה

חישוב עכבת המעגל במעגל טורי המתואר באיור 12.5:

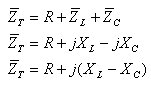
בתהודה היגב הקבל שווה להיגב הסליל:

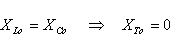
מכאן מתקבל שעכבת המעגל בתהודה שווה לנגד R:

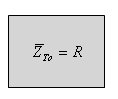
כלומר במעגל המצוי בתהודה, מקור האנרגיה "רואה" אך ורק את ההתנגדות הטהורה, השווה להתנגדות הנגד. כמו כן אפשר לומר שבמעגל טורי עכבת המעגל, במצב של תהודה, היא מינימלית. בכל תדר אחר סביב לתדר התהודה יש היגב שקול של הסליל והקבל, הנוסף להתנגדות הנגד ומעלה את גודל העכבה.

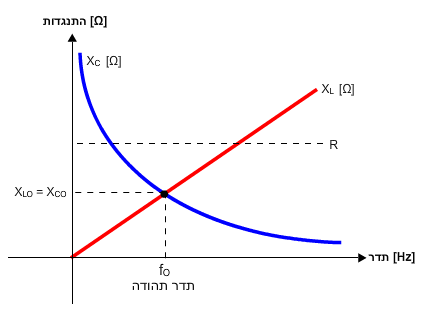
אפשר לתאר את השתנות העכבה כתלות בתדר בעזרת איור 12.7.

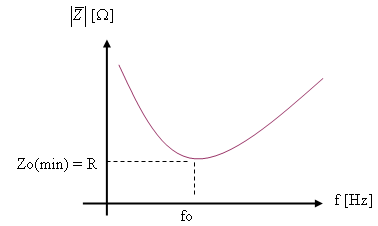
איור 12.7

אם נשנה את גודל הנגד R נראה שמגמת שינוי העכבה לא תשתנה, אך שינוי גודל הנגד ישפיע גם על פיסוקו של הגרף וגם על מיקומה של נקודת הקיצון המינימלית (Zo(min

שינוי ערך התנגדות הנגד משפיע על מיקום הגרף ופיסוקו. שנו את התנגדות הנגד והיווכחו בתוצאות.

הסבר לאופיין:

אם נשנה את ערך הנגד R, תדר התהודה יישאר קבוע. כלומר, לנגד אין משמעות בקביעת תדר התהודה של המעגל.

מאחר שעכבת המעגל בתהודה שווה להתנגדות הנגד, הרי שעם הגדלת ערך הנגד נקודת הקיצון בגרף  עולה גם כן ולהפך כשמקטינים את ערך הנגד (נקודת הקיצון מתארת את העכבה של המעגל בתהודה).

דבר נוסף שמשתנה עם שינוי ערך הנגד הוא הפיסוק של הגרף, לשינוי זה יש משמעות בנוגע לאיכות המעגל - על כך נדון בהמשך!

הזרם בתהודה

חישוב הזרם במעגל יהיה על פי חוק אום:

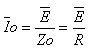
ואם ידוע שבתהודה העכבה מינימלית, משמעות הדבר שהזרם מקסימלי (יחס הפוך).

את השתנות הזרם במעגל כתלות בתדר המקור אפשר לתאר בעזרת איור 12.8:

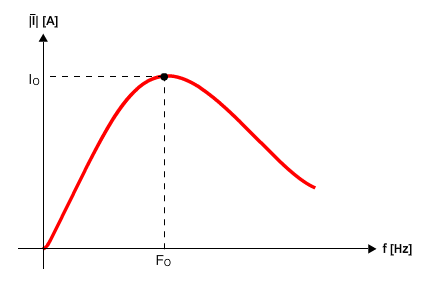
איור 12.8

הסבר לאופיין:

מאחר שבתהודה העכבה מינימלית - הזרם הוא מקסימלי.

בתדרים נמוכים מאוד (אפס) וגבוהים מאוד (אינסוף), עכבת המעגל שואפת לאינסוף לכן הזרם שואף לאפס.

פאזורי המתחים בתהודה

על פירוק המתחים של קירכהוף:

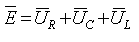
בתהודה, כאמור, היגב הקבל שווה להיגב הסליל. מאחר שהזרם שווה ברכיבים טוריים, גם המתח על הקבל שווה בגודלו למתח על הסליל (קיים היפוך מופע של 180°). כלומר המתח הכולל על הקבל והסליל יחד שווה לאפס. הקבל והסליל בתהודה טורית הופכים לקצר.

לכן אפשר לומר שבתהודה טורית כל מתח המקור "נופל" על הנגד R.

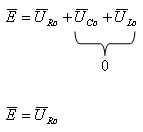
נתאר את פאזורי המתח בתהודה, על פני רכיבי המעגל באיור 12.9:

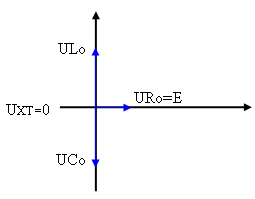
איור 12.9 

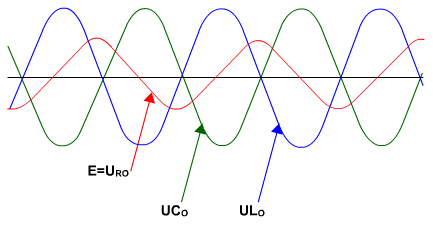
איור 12.10

אפשר לראות שהמתח על הסליל שווה למתח על הקבל, אך בהיפוך מופע של º180.

זווית המופע בתהודה

זווית המופע במעגל מוגדרת כהפרש המופע בין המתח לזרם במעגל. זווית זו מתארת את זווית העכבה.

מאחר שידוע שבתהודה עכבת המעגל היא התנגדות אוהמית טהורה, הרי שזווית המופע היא אפס.

זו הסיבה לכך שבתהודה אין הפרש מופע בין המתח לזרם במעגל.

כדי לנתח את תלות זווית המופע בתדר, ניעזר שוב באופיין 12.6:

את השתנות המופע של הזרם לעומת המתח במעגל, כתלות בתדר המקור,אפשר לתאר באמצעות איור 12.11.

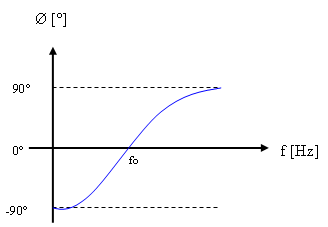
איור 12.11

הסבר לאופיין:

בתדרים הקטנים מתדר התהודה זווית המופע שלילית, כי היגב הקבל גדול מהיגב הסליל. בתדר השווה לאפס (מתח ישר) היגב הקבל הוא אינסופי, כלומר המקור "רואה" רק קבל (זווית -90°). עם הגדלת התדר, היגב זה קטן ולכן זווית המופע קטנה גם כן.

בתדר השווה לתדר התהודה, זווית המופע שווה לאפס, כי היגב הסליל והיגב הקבל שווים בגודלם והפוכים בסימן ולכן הם מבטלים זה את זה.

בתדרים הגבוהים מתדר התהודה זווית המופע חיובית, כי היגב הסליל גדול מהיגב הקבל. בתדר גבוה מאוד (אינסופי) היגב הסליל הוא אינסופי, כלומר המקור "רואה" רק סליל (זווית 90°).

חישוב תדר התהודה

 כאמור, בתהודה היגב הקבל שווה בגודלו להיגב הסליל. לכן:

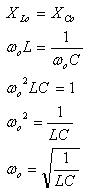
כלומר תדירות זוויתית תהודתית אפשר לחשב כך:

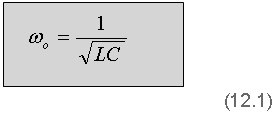
ידוע הקשר בין תדירות זוויתית לבין תדר: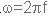לכן:

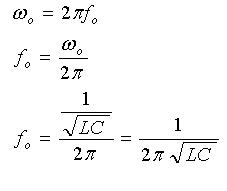
תדר התהודה במעגל טורי יחושב כך:

•   הקודם                                                                                                                             
• המשך