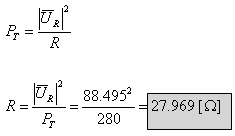קורס בתורת החשמל מאת יוסי יאשי

תרגיל דוגמה 14

במעגל שמתואר באיור 11.45 ידוע פאזור הזרם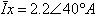 

איור 11.45

חשבו את:

א. פאזור מתח המקור;

ב. מתירות המעגל;

ג. קבעו את אופי המעגל. נמקו את תשובתכם;

ד. ההספקים הכוללים - סרטטו משולש הספקים;

ה. ערכי העכבה Z1.

פתרון תרגיל דוגמה 14

א. נחשב את העכבה השקולה של הנגד R והסליל L1 שמחוברים במקביל - עכבה זו תיקרא Z2.

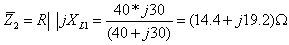
נציג את המעגל השקול כמתואר באיור 11.46.

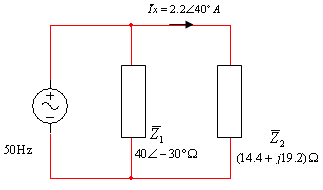
איור 11.46

ב. על פי חוק הזרמים של קירכהוף נחשב את פאזור זרם המקור:

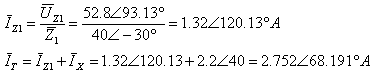
על פי חוק אוהם נקבל:

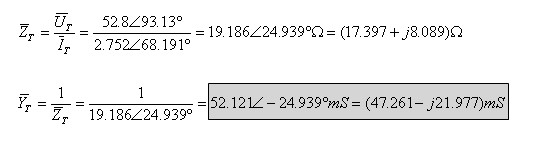
ד. לצורך חישוב ההספקים הכוללים של המעגל נציג את עכבת המעגל - איור 11.47.

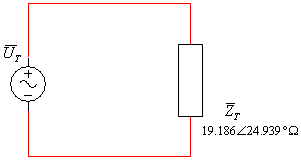
איור 11.47

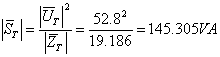
זווית העכבה שווה לזווית ההספק המדומה לכן:

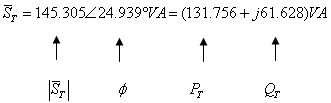
משולש הספקים למעגל - איור 11.48

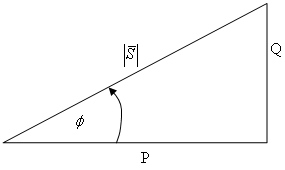
איור 11.48

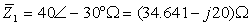
כלומר העכבה Z1 מכילה נגד שערכו 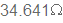בטור עם קבל שהיגבו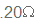 

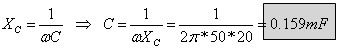
תרגיל דוגמה 15

במעגל שמתואר באיור 11.49 נתונים ערכי הזרם דרך כל אחד מרכיבי המעגל.

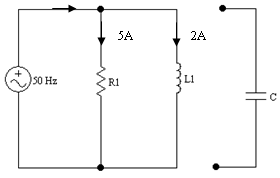
איור 11.49

חשבו את:

א. הזרם שמספק מקור המתח;

ב. ההספק הכולל במעגל הנו 400W. חשבו את מתח המקור;

ג. רכיבי המעגל R ו- L;

ד. מתירות המעגל;

ה. מחברים קבל בעל היגב של Ω60 במקביל לרשת. קבעו את אופי המעגל. נמקו תשובתכם!

פתרון תרגיל דוגמה 15

על פי חוק הזרמים של קירכהוף סכום הזרמים דרך כל אחד מן הרכיבים שווה לזרם המקור. אך יש לזכור שחיבור זה הנו חיבור וקטורי (פאזורי).

הזרמים הנתונים דרך רכיבי המעגל הנם גדלים וקטורים, לכן אין אנו יכולים לחבר ביניהם  חיבור חשבוני פשוט.

המתח על הנגד והסליל שווה למתח המקור. נניח, לצורך ההסבר, שמתח המקור הוא בזווית של אפס מעלות. במקרה זה נקבל שפאזורי הזרם דרך כל אחד מן הרכיבים:

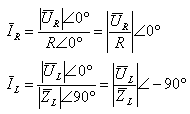
נסרטט שני פאזורים אלה על גבי דיאגרמת וקטורים ונבצע חיבור וקטורי ביניהם לקבלת הזרם הכללי - איור 11.50.

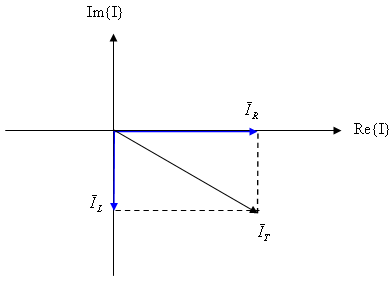
איור 11.50

מאחר שבין שני פאזורי הזרם (זרם הסליל וזרם הנגד) קיימת זווית של 90º, החיבור הווקטורי ביניהם יוצר משולש ישר זווית, שהיתר שבו מתאר את הזרם הכללי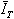 

א. לכן אפשר לחשב את הזרם הכולל, שמספק מקור המתח, על פי פיתגורס:

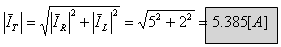
הערה:

הפרש של 90º בין פאזור הזרם בנגד לבין פאזור הזרם בסליל יהיה גם אם זווית מתח המקור תהיה שונה מאפס. ראו דוגמה באיור 11.51 שבה זווית מתח המקור היא כ- º30.

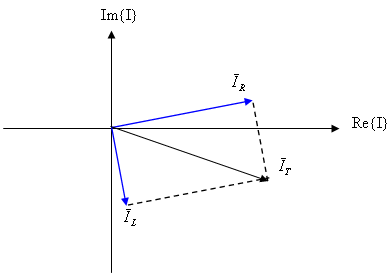
איור 11.51

ב. נתון שההספק הכולל הנו 400W. לפי היחידות "ואט" אנו מבינים שמדובר בהספק הפעיל הכולל במעגל  PT=400W. הספק זה מתפתח על פני הנגד R בלבד, לכן:

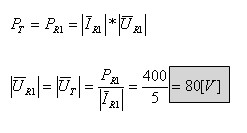
ג. נחשב את התנגדות רכיבי המעגל על פי חוק אוהם

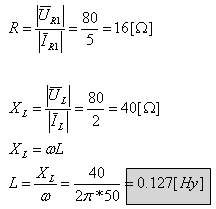
ד. את מתירות המעגל לא נוכל לחשב באמצעות חוק אוהם כי, בשלב זה, אנו יודעים אך ורק גדלים וקטורים של מתח וזרם המקור. לכן במקרה זה נחשב את מתירות המעגל באמצעות התנגדויות המעגל.

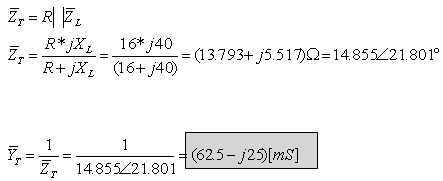
ה. נחשב את עכבת המעגל לשם קביעת אופי המעגל

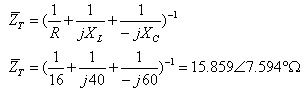
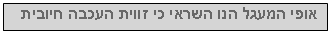
הערה:

יש לשים לב שהיגב הקבל גדול יותר מהיגב הסליל ובכל זאת אופי המעגל הנו השראי (הפוך מאשר במעגל טורי). כדי שלא  לטעות, מומלץ לקבוע את אופי המעגל דרך זווית העכבה, שכן אם היא חיובית אופי המעגל השראי ואם היא שלילית אופי המעגל קיבולי.

תרגיל דוגמה 16

במעגל שמתואר באיור 11.52 נתון כי ההספק הכולל במעגל הנו  750VA.

חשבו את מתח המקור.

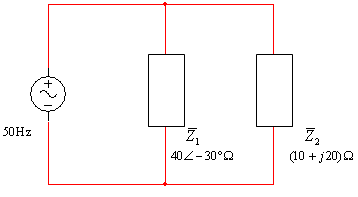
איור 11.52

פתרון תרגיל דוגמה 16

ההספק הכולל שנתון בשאלה מתפתח על העכבה השקולה של המעגל. לכן, נחשב תחילה את עכבת המעגל:

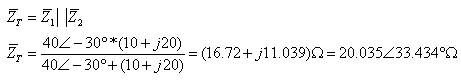
בנוסחאות ההספקים אנו מציבים רק גדלים וקטורים:

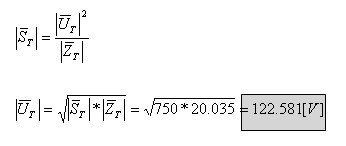
תרגיל דוגמה 17

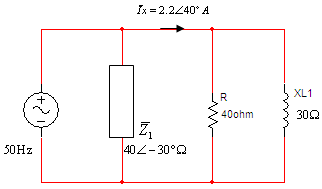
במעגל שמתואר באיור 11.53 ידוע שהזרם מקדים את המתח ב- º40.

ההספק הפעיל הכולל במעגל הנו 280W.

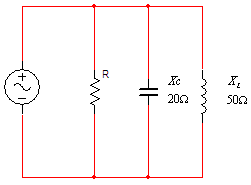
איור 11.53

חשבו את:

א. מתח המקור;

ב. גודל הנגד R.

פתרון תרגיל דוגמה 17

א. על סמך נתוני השאלה נסרטט תחילה משולש הספקים המתאים למעגל שבאיור 11.53. היות שהזרם מקדים את המתח אופי המעגל הוא קיבולי, כלומר זווית ההספק המדומה שלילית.

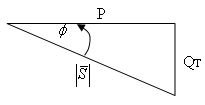
איור 11.54

נחשב את ההספק העיוור הכולל במעגל:

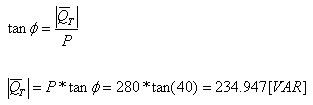
נחשב את ההיגב השקול של הסליל והקבל יחד:

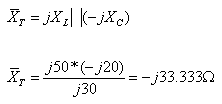
נסרטט מעגל שקול לזה שמתואר באיור 11.53.

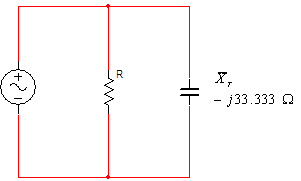
איור 11.55

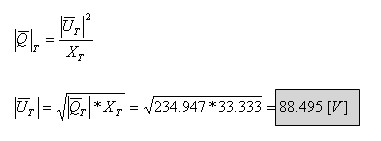
ב. כעת נוכל לחשב את גודל הנגד R במעגל:

•   הקודם                                                                                                                             
• המשך