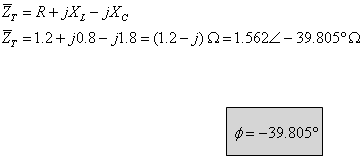קורס בתורת החשמל מאת יוסי יאשי

תרגיל דוגמה 9

במעגל שמתואר באיור 11.30 מחובר סליל ממשי בעל השראות של 80mH והתנגדות של  .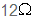

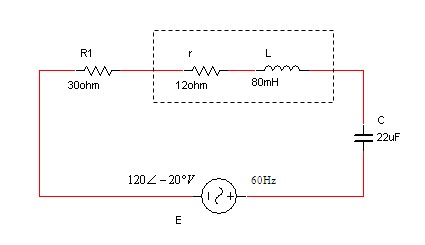
איור 11.30

חשבו את:

א. פאזור המתח על פני הסליל הממשי;

ב. ההספק הממוצע הנצרך על ידי הסליל הממשי;

ג. ההספק המתפתח בנגד R1 ובקבל C'

ד. ההספקים הכוללים במעגל (פעיל, היגבי ומדומה) - סרטטו משולש הספקים.

פתרון תרגיל דוגמה 9

יש לשים לב, בפתרון השאלה, שנתון סליל מעשי. בכל פעם שיצוין הביטוי הזה הכוונה היא שהסליל כולל גם השראות וגם התנגדות חוטים ולכן אפשר להציגו כשני רכיבים שמחוברים בטור (נגד r בעל התנגדות של 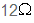 ומשרן של 80mH).

א. לצורך חישוב פאזור הזרם במעגל נחשב את היגבי המעגל:

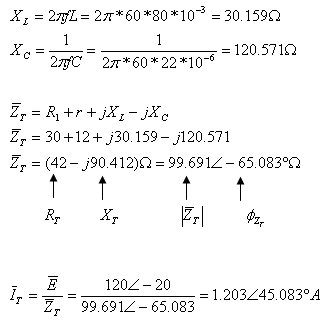
חישוב פאזור המתח על הסליל הממשי: 

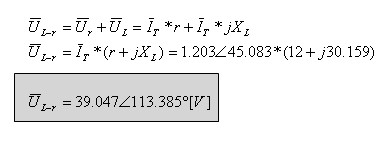
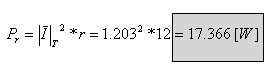
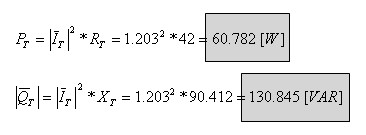
ג. חישוב ההספק הפעיל המתפתח בנגד R1:

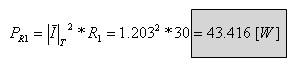
חישוב ההספק ההיגבי המתפתח בקבל C1:

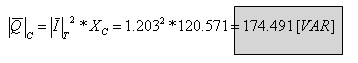
הערה:

את ההספק העיוור בקבל אפשר גם להציג במישור המרוכב כך:

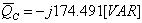
המשך פתרון תרגיל דוגמה 9

ד. חישוב ההספקים הכוללים במעגל:

יש דרכים שונות לחשב את ההספקים הכוללים במעגל:

דרך ראשונה - באמצעות עכבת המעגל

נבחן את תוצאת עכבת המעגל שהתקבלה תוך כדי פתרון התרגיל:

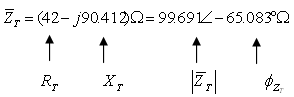
הערה:

את ההספק העיוור הכולל במעגל אפשר גם להציג במישור המרוכב כך: 

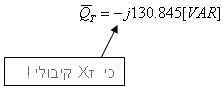
חישוב ההספק המדומה הכולל במעגל:

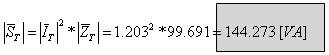
הערה:

את ההספק המדומה של המעגל אפשר גם להציג במישור המרוכב כך:

דרך שנייה - סכום ההספקים

כדי למצוא ההספק הפעיל הכולל, במעגל, נחבר בין כל ההספקים הפעילים על פני רכיבי המעגל (נגדים):

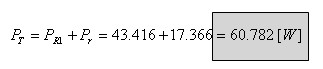
כדי למצוא ההספק העיוור הכולל, במעגל, נחבר וקטורית בין כל ההספקים העיוורים על פני רכיבי המעגל (סלילים וקבלים):

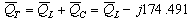
נחשב את ההספק העיוור על המשרן L:

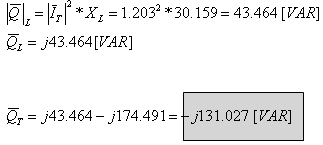
כדי למצוא את ההספק המדומה במעגל, נחבר וקטורית בין ההספק הפעיל הכולל לבין ההספק העיוור הכולל:

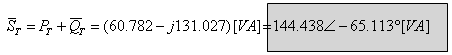
אפשר להיווכח בכך שזווית ההספק המדומה זהה לזווית העכבה!

דרך שלישית - באמצעות חישוב ישיר של ההספק המדומה והצגתו בצורה פולארית וקרטזית

נחשב את ההספק המדומה הכולל:

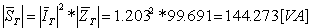
נציג את ההספק המדומה כווקטור בצורתו הפולארית (נוסיף לגודל את זווית העכבה):

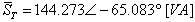
נציג ערך זה גם בצורה קרטזית:

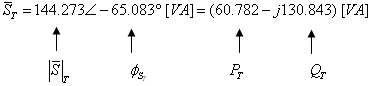
משולש הספקים של המעגל:

נציג את ההספקים הכוללים על גבי מערכת צירים במישור המרוכב ונקבל משולש הספקים כמתואר באיור 11.31

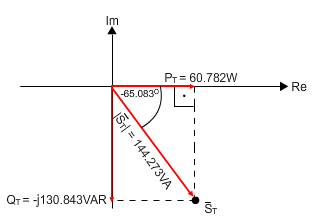
איור 11.31

היות שמדובר במשולש ישר זווית, אפשר להוציא גם את הקשרים הטריגונומטריים האלה:

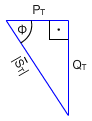
איור 11.32

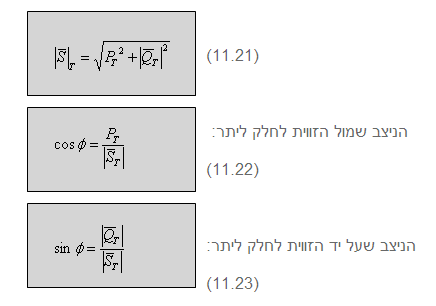
על פי משפט פיתגורס:

הערות:

1.     הזווית 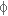 מתייחסת אמנם לזווית ההספק המדומה, אך היא שווה גם לזווית המופע במעגל - זווית העכבה.

2. הערך של 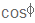 נקרא בשם גורם ההספק ולו חשיבות רבה בתחום מערכות ההספק, נלמד עליו בהמשך הפרק.

3. במעגל בעל אופי השראי, יתקבל משולש הספקים כשהוא  מעל הציר הממשי, ברביע הראשון של המישור המדומה (זווית חיובית).

4. אפשר להיעזר במשוואות 11.21-11.23 לחישוב הספקים במעגלי זרם חילופין.

ממשוואות 11.22 ו- 11.23 נובע:

ניעזר במשוואה 11.18:

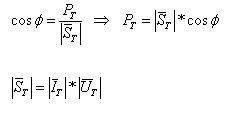
נציב ונקבל משוואה נוספת (11.24) לחישוב ההספק הפעיל

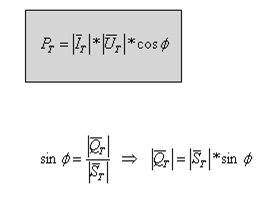
ניעזר במשוואה 11.18: 

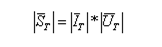
נציב ונקבל משוואה נוספת (11.25) לחישוב ההספק העיוור 

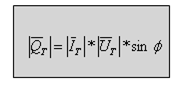
את ההספק המדומה אפשר לחשב גם באמצעות משוואה 11.26:

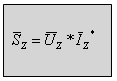
(11.26) 

כאשר:

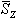- ההספק המדומה כווקטור, שיחידותיו [VA]

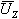- פאזור המתח על העכבה, ביחידות [V]

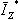- הצמוד של פאזור הזרם דרך העכבה היחידות הן [A]

תרגיל דוגמה 10

במעגל שמתואר באיור 11.33 המתח מקדים את הזרם ב-60°.

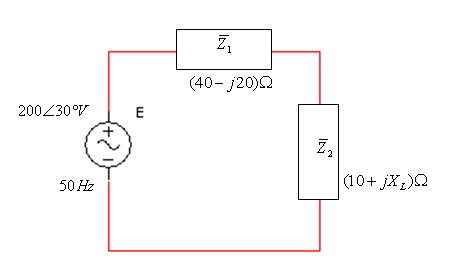
איור 11.33

חשבו את:

א. גודל המשרן שמחובר בתוך העכבה ;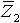

ב. פאזור המתח על פני העכבה ;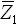

ג. הספק הנמסר על ידי מקור המתח.

פתרון תרגיל דוגמה 10

א. נבטא את עכבת המעגל:

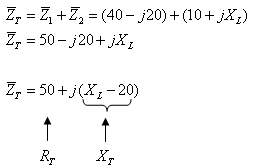
נתון שהמתח מקדים את הזרם ב- 60°. מכאן אפשר להסיק שזווית העכבה חיובית ושווה 60°. נסרטט משולש התנגדויות למעגל - איור 11.34:

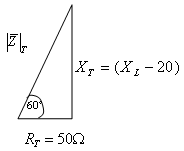
איור 11.34

נחשב את הניצב TX על ידי שימוש ב- tan:

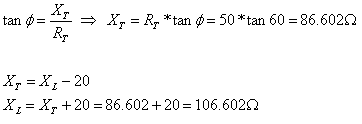
חישוב גודל המשרן L:

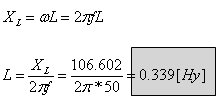
ב. נחשב את עכבת המעגל:

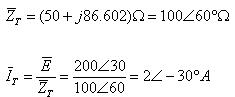
חישוב פאזור המתח על פני העכבה :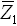

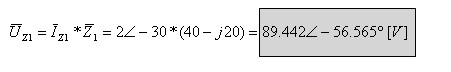
ג. לחישוב ההספק הכולל שנמסר על ידי מקור המתח ניעזר במשוואה 11.26:

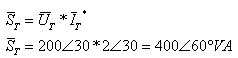
נציג את שלושת סוגי ההספקים שנמסרים

על ידי מקור המתח:

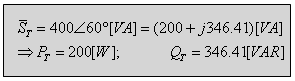
תרגיל דוגמה 11

ההספק הכולל במעגל שבאיור 11.35 שווה ל- 480W.

איור 11.35

חשבו את:

א. מתח המקור;

ב. ההספק בנגד R2 ובסליל XL1;

ג. הזרם דרך הקבל XC2.

פתרון תרגיל דוגמה 11

א. נחשב את עכבת המעגל :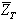

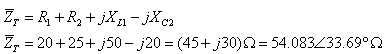
נסרטט מעגל שקול לרשת שבאיור 11.35:

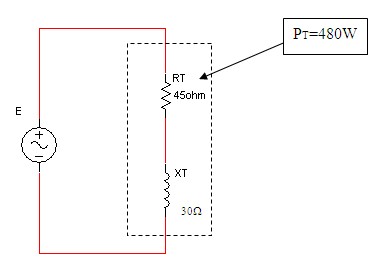
איור 11.36 

שימו לב! באמצעות ההספק הפעיל הכולל שנתון TP וההתנגדות הטהורה השקולה TR אפשר כמובן לחשב מתח, אך מתח זה אינו מתח המקור, אלא המתח שנופל על הנגד השקול RT.

אם נדע מהו ההספק הכולל שמתפתח בעכבה , נוכל לחשב את מתח המקור, מאחר שאנו יודעים את גודלה של העכבה .

ניעזר בקשרים שקיימים במשולש ההספקים (נוסחה 11.22):

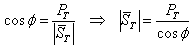
הזווית 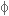 מתארת את זווית המופע במעגל - זווית העכבה!

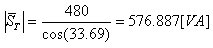
כעת נוכל לחשב את מתח המקור:

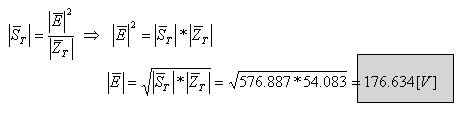
הערה: בחישוב ההספקים בזרם חילופין אנו מציבים גדלים בלבד (פרט לנוסחה 11.26) וזו הסיבה שהתקבל גודלו של מתח המקור. אין זה עומד בסתירה לסעיף א' שבו אנו נדרשים לחשב את "מתח המקור" (כלומר את ערכו בלבד) ולא את "פאזור מתח המקור".

אי אפשר לחשב את פאזור מתח המקור, כל זמן שאין אנו יודעים את זווית הזרם במעגל.

ב. נחשב את עצמת הזרם במעגל (לא פאזור - גודל בלבד)

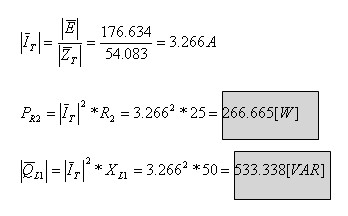
ג.

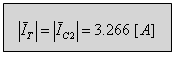
תרגיל דוגמה 12

מד המתח שבאיור 11.37 מראה 40 וולט.

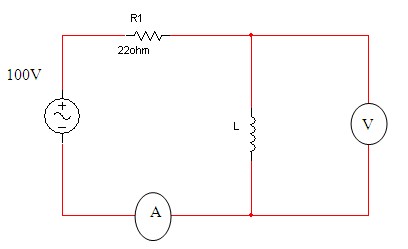
איור 11.37

חשבו :

א. מה מראה מד הזרם?

ב. את ההספק המדומה הכולל במעגל;

ג. את גודלו של המשרן L, אם ידוע שתדר המקור 50Hz.

פתרון תרגיל דוגמה 12

א. נרכז את נתוני השאלה - יש לשים לב כי המתחים נתונים כגדלים בלבד:

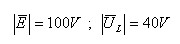
כאמור, אי אפשר לחסר בין הגדלים לקבלת גודל המתח על הנגד R1.

מאחר שהזרם שעובר בסליל ובנגד זהה מתפתח על כל אחד מן הרכיבים, המתח והפרש הזוויות ביניהם הוא 90°.

איור 12.38 מתאר את החיבור הווקטורי בין שני המתחים, הצורה ההנדסית שהתקבלה היא מלבן. במקרה זה, מתואר המתח על הנגד עם זווית שלילית, שזו גם הזווית של הזרם.

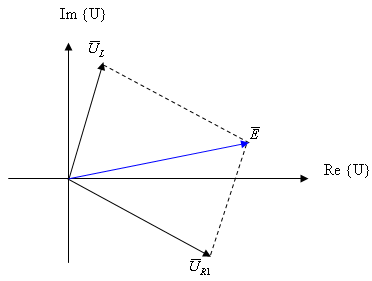
איור 11.38

במקרה שבו יש הפרש של 90° בין שני הווקטורים, אפשר להיעזר במשפט פיתגורס למתחים במשולש ישר זווית:

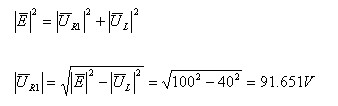
הפתרון, משלב זה ואילך, יהיה אך ורק עם גדלים (חישוב פאזורים אפשרי רק אם מניחים זווית ייחוס, לזרם למשל - לא מומלץ! אפשר לפתור ללא כל צורך בכל מיני הנחות).

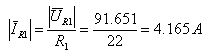
ב. את ההספק המדומה נחשב, בשלב זה, כגודל בלבד:

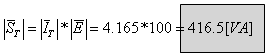
ג. נחשב את התנגדות הסליל (היגב), על פי חוק אוהם:

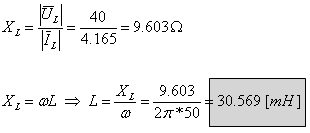
תרגיל דוגמה 13

באיור 11.39 מתואר תרשים מתחים של מעגל RLC טורי בזרם חילופין.

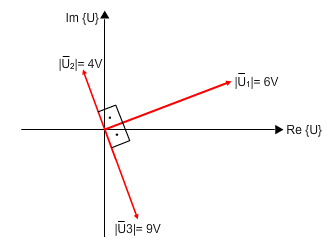
איור 11.39

א. חשבו את מתח המקור;

ב. קבעו את אופי המעגל (השראי או קיבולי).נמקו תשובתכם!

ג. ההספק העיוור במעגל שווה 25VAR. חשבו את גודל כל אחד מהרכיבים R, L ו- C (תדר הרשת 50Hz;)

ד. חשבו את זווית המופע במעגל.

פתרון תרגיל דוגמה 13 

באיור 11.39 נתונים הגדלים של המתחים על כל אחד מן הרכיבים R, L ו- C. נתאים בין כל אחד מן הנתונים לרכיבי המעגל.

יש להתאים בין המתחים:

המתחים של הקבל והסליל "רוכבים" על אותו ישר ובכיוונים הפוכים, לכן אפשר לבצע קיזוז ביניהם לקבלת מתח שקול על פני הסליל והקבל יחד:

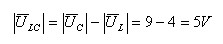
נחבר בצורה וקטורית בין המתח השקול של הקבל והסליל לבין המתח של הנגד כמתואר באיור 11.40: 

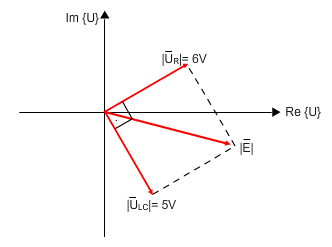
איור 11.40

חישוב מתח המקור באמצעות משפט פיתגורס:

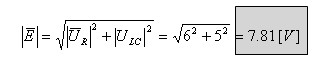
ב. במעגל שנתון בשאלה עובר זרם בעצמה זהה דרך כל אחד מן הרכיבים (מעגל טורי). מן התרשים שבאיור 12.39 הסקנו שהמתח על הקבל גדול יותר מן המתח על הסליל. עובדה זו היא תוצאה של היגב קבל שגדול יותר מהיגב הסליל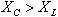 

ג. ההספק העיוור הכולל במעגל מתפתח על הקבל ועל הסליל יחד. נחשב את הזרם הכללי במעגל:

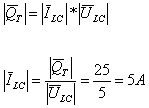
באמצעות חוק אוהם נחשב את התנגדות כל אחד מרכיבי המעגל:                

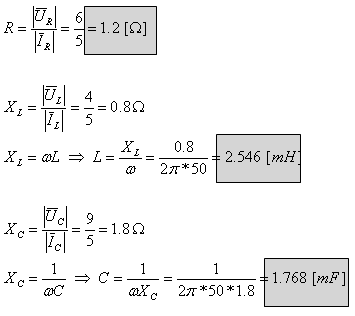
ד. זווית המופע במעגל מבטאת את זווית העכבה

•   הקודם                                                                                                                             
• המשך