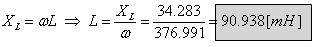קורס בתורת החשמל מאת יוסי יאשי

תרגיל דוגמה 7

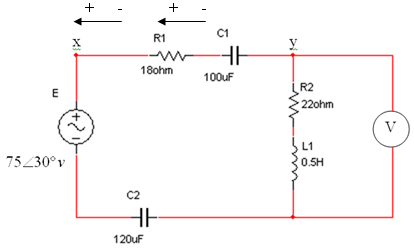
נתון המעגל שבאיור 11.19 (תדר המקור 50Hz).

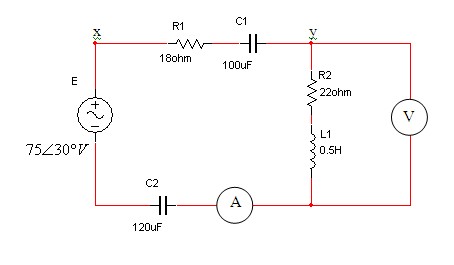
איור 11.19

חשבו את:

א. עכבת המעגל וסרטטו משולש התנגדויות;

ב. קריאות כל אחד ממכשירי המדידה;

ג. פאזור המתח Uxy;

ד. קבעו את אופי המעגל, (השראי, קיבולי, או התנגדותי) נמקו את תשובתכם.

פתרון תרגיל דוגמה 7

נחשב את היגבי הרכיבים במעגל:

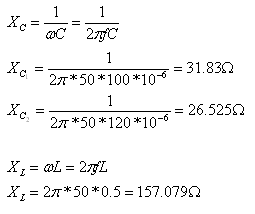
את עכבת המעגל נחשב כסכום ההתנגדויות במעגל הטורי:

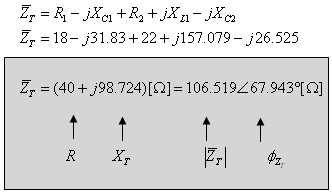
נסרטט משולש התנגדויות למעגל כמתואר באיור 11.20:

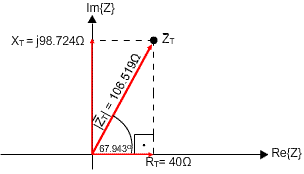
איור 11.20

ב. נחשב את פאזור זרם המקור:

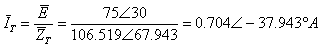
כדי לחשב את קריאת מד המתח נחשב תחילה את פאזורי המתח על הנגד R2 והסליל L1:

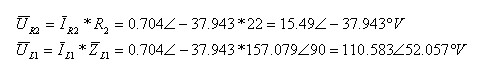
מד המתח אמנם מראה רק את גודל המתח על שני הרכיבים, R2 ו- L1, יחד, אך חשוב לזכור שאי אפשר לחבר, ככה סתם, בין גודלי המתח של הרכיבים R2 ו- L1. יש לפעול בשלוש דרכים:

דרך ראשונה - חיבור וקטורי בין המתחים

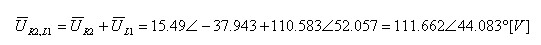
דרך שנייה - חיבור הגדלים באמצעות משפט פיתגורס

נציג את פאזורי המתח על פני הנגד R2 והסליל L1 על גבי תרשים פאזורי כמתואר באיור 11.21.

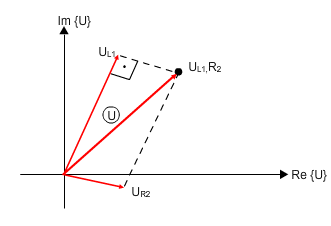
איור 11.21

היות שבין שני הגדלים האלה קיימת זווית של 90° אפשר להיעזר במשפט פיתגורס.

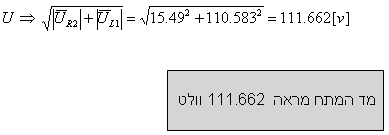
דרך שלישית - שימוש בכלל מחלק המתח

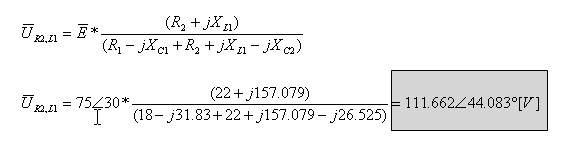
ג. נבחר מסלול קצר לחישוב פאזור המתח Uxy - איור 11.22

איור 11.22

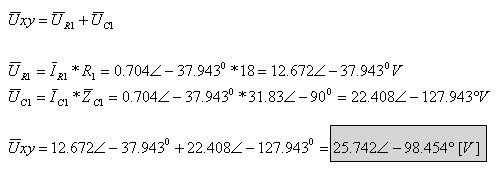
ד. המעגל יכול להיות בעל אופי התנגדותי, קיבולי או השראי. בהתאם לזווית המופע במעגל (זווית העכבה) אפשר לדעת מהו אופי המעגל, כפי שמסוכם בטבלה שלפניכם:

תרגיל דוגמה 8

נתון מעגל בזרם חילופין כמתואר באיור 11.23

הזרם במעגל נתון באמצעות הביטוי המתמטי: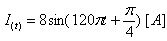 

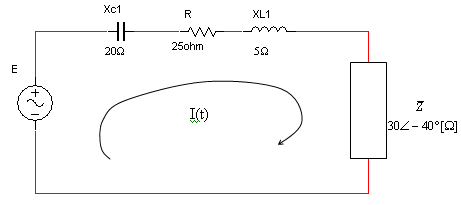
איור 11.23

חשבו את:

א. פאזור מתח המקור;

ב. זווית המופע במעגל;

ג. ערכי העכבה Z;

ד. מחברים בטור למעגל רכיב נוסף שגורם לזווית המופע להתאפס (אופי התנגדותי). קבעו מהו הרכיב שחובר וחשבו את גודלו.

פתרון תרגיל דוגמה 8

א. ראשית נציג את אות הזרם כערך יעיל ובצורה פאזורית:

2. התדירות הזוויתית 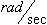 של אות הזרם (ביחידות של ) שווה:

כלומר פאזור הזרם במעגל הוא: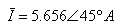 

נחשב את עכבת המעגל:

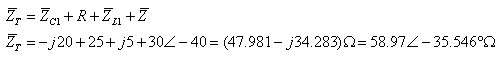
על פי חוק אוהם:

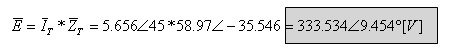
ב. זווית המופע במעגל, זו בעצם זווית העכבה הכללית, היא מתארת את הפרש המופע בין המתח לזרם במעגל!

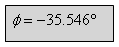
ג. בתוך ה"קופסה" 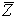 יש שני רכיבים המחוברים בטור. לפי זווית העכבה אפשר להבין באילו רכיבים מדובר:

כדי למצוא את ערכי העכבה 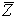 נציג אותה בצורה קרטזית:

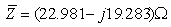
כלומר בתוך העכבה יש נגד שערכו 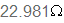 המחובר בטור עם קבל שהיגבו, בתדר הנתון, הוא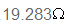

נחשב את קיבול הקבל עצמו:

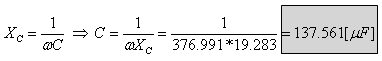
ד. כדי להביא את המעגל לכך שיהיה בעל אופי התנגדותי עלינו לבחון את עכבת המעגל במצב הנתון:

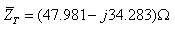
נחשב את גודל המשרן שיש לחבר בטור למעגל:

•   הקודם                                                                                                                            
•  המשך