(RL series circuits)
במעגל זה מחוברים, אל מקור המתח החילופין, נגד בטור עם סליל כמתואר
באיור 11.1.
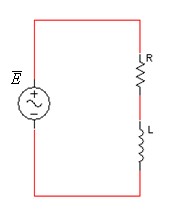
איור 11.1
כאמור על פי מאפייני המעגל הטורי במעגל שמוצג באיור 11.1 מתקיים:
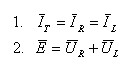
הערה:
יש לשים לב שהחיבור הנו חיבור בין וקטורים (פאזורים) ולא חיבור
רגיל!
העכבה במעגל RL טורי
נבדוק מה ההתנגדות ש"רואה" מקור המתח במעגל שבאיור 11.1:
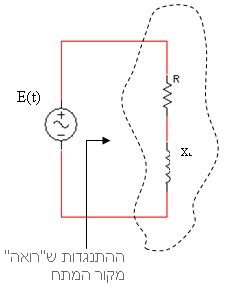
איור 11.1
מתח המקור מרגיש שתי
התנגדויות המחוברות בטור ביניהן, האחת ממשית R והשנייה דמיונית XL. בחיבור טורי אפשר
לחבר בין ההתנגדויות למציאת התנגדות כוללת. חיבור בין שתי התנגדויות אלה ייתן
התנגדות מרוכבת הנקראת בשם עכבה 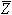 .
.
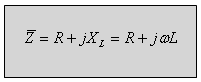
(12.1)
העכבה 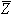 מציגה התנגדות במישור המרוכב ולכן
העכבה שרואה מקור המתח, נקראת גם בשם עכבת
המעגל והיא מתארת את היחס בין פאזור מתח המקור לבין פאזור זרם
המקור - יחידות העכבה [
מציגה התנגדות במישור המרוכב ולכן
העכבה שרואה מקור המתח, נקראת גם בשם עכבת
המעגל והיא מתארת את היחס בין פאזור מתח המקור לבין פאזור זרם
המקור - יחידות העכבה [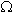 ].
].
הערה
ידוע שלנגד יש התנגדות R, ואילו לסליל יש התנגדות (היגב) 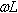 . לכל אחד מרכיבים אלה
יש גם עכבה, כלומר אפשר להציג את ההתנגדויות של אותם רכיבים במישור המרוכב:
. לכל אחד מרכיבים אלה
יש גם עכבה, כלומר אפשר להציג את ההתנגדויות של אותם רכיבים במישור המרוכב:
|
התנגדות
הרכיב במעגלי זרם חילופין
|
הצגת
התנגדות הרכיב במישור המרוכב
|
|
נגד
|
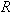
|
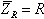
|
|
סליל
|
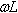
|
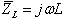
|
את המעגל שבאיור 11.1 אפשר להציג באמצעות עכבה כמתואר באיור 11.2.
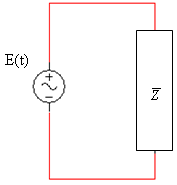
איור 11.2
הערה:
בכל מקרה שנציג "קופסה סגורה" באמצעות העכבה  , הכוונה היא
לרכיבים המחוברים
בטור ביניהם.
, הכוונה היא
לרכיבים המחוברים
בטור ביניהם.
משולש התנגדויות במעגל RL טורי
אפשר להציג את ההתנגדויות שמתוארות במעגל שבאיור 11.1 במישור
המרוכב ולקבל משולש הנקרא בשם משולש התנגדויות.
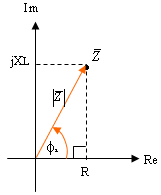
איור 11.3
מן המשולש שמתואר באיור 11.3 אפשר להגיע לנוסחאות שלפניכם,
המתקיימות במשולש ישר זווית:
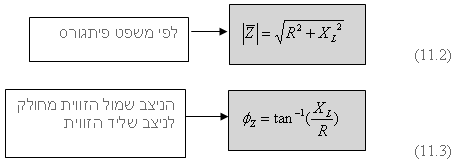
באמצעות משוואה (11.2) אפשר לחשב את היתר במשולש ישר הזווית - גודל
העכבה.
באמצעות משוואה (11.3) אפשר לחשב את הזווית במשולש ישר הזווית -
זווית העכבה.