קורס בתורת החשמל מאת יוסי יאשי

(Basic arithmetic on complex numbers)

בפתרון של רשתות בזרם חילופין המכילות מקורות מתח סינוסואידליים נמצא את עצמנו רושמים את חוק אום בצורה פולארית, או רושמים את חוק המתחים של קירכהוף בצורה מרוכבת. שימוש בפעולות חשבון בסיסיות בפתרון של רשתות בזרם חילופין הוא פעולה הכרחית ביותר לניתוח הרשתות האלה.

נתמקד בארבע פעולות החשבון הבסיסיות ביותר: חיבור, חיסור, כפל וחילוק בין מספרים מרוכבים.

הערה: אפשר להיעזר במחשבון  בפעולות החשבוניות האלה.

פעולת חיבור בין מספרים מרוכבים

בצורה קרטזית:

חיבור בין שני מספרים בצורה קרטזית מתבצע כמו כינוס אברים דומים: מכנסים את המספרים הממשיים לחוד ואת המספרים הדמיוניים לחוד. 

לדוגמה נתונים שני המספרים האלה: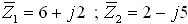 

דרוש לחשב: 

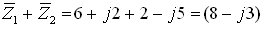
נתונים שני המספרים האלה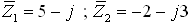 

מחברים בין שני מספרים אלה. 

בצורה פולארית:

חיבור בין שני מספרים בצורה פולארית פירושו חיבור בין שני וקטורים. כדי לחבר באופן גרפי בין שני וקטורים יש ליצור מקבילית, או לפרק את הווקטורים להיטלים כמתואר בפרקי המבוא בפיסיקה.

פירוק להיטלים פירושו להמיר את המספרים המרוכבים שבצורה פולארית לצורה קרטזית, לכנס אברים דומים (ממשי עם ממשי ודמיוני עם דמיוני) ואת התוצאה להחזיר שוב לצורה הפולארית.

לדוגמה נתונים שני המספרים האלה: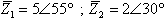 

דרוש לחשב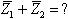 

נציג תחילה פתרון גרפי לתרגיל:

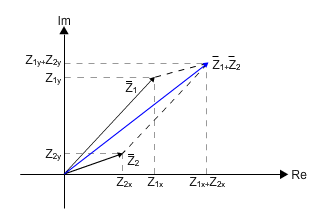
איור 10.42

המספרים המרוכבים 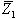 ו-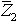 פורקו להיטלים (הומרו לצורה קרטזית) כדי שיהיה אפשר לחבר ביניהם באופן פשוט. וקטור תוצאת החיבור הנו החץ שיוצא מקדקוד מערכת הצירים אל פינת המקבילית שנוצרה. 

נבצע חיבור בין שני המספרים 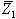 ו-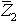 - נמיר את המספרים המרוכבים שבצורה פולארית לצורה קרטזית, נכנס אברים דומים (ממשי עם ממשי ודמיוני עם דמיוני) ואת התוצאה נחזיר שוב לצורה הפולארית. במחשבון ניעזר כדי לעבור מצורה אחת לאחרת באופן מהיר.

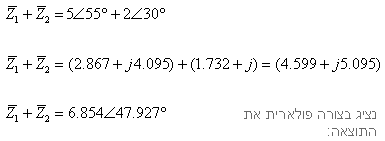
נתונים שני המספרים האלה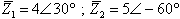מחברים בין שני מספרים אלה.

הערה: פעולת חיבור בין שני מספרים מרוכבים בצורה פולארית בעלי אותה זווית תיתן מספר פולארי בעל אותה זווית וגודלו הווקטורי הוא סכום של הגדלים הווקטורים של כל אחד מן המספרים שחוברו:

•   הקודם                                                                                                                             
• המשך