קורס בתורת החשמל מאת יוסי יאשי

(The connection between polar and Cartesian form)

אפשר לעבור מצורה קרטזית לצורה פולארית ולהפך באמצעות קשרים טריגונומטריים.

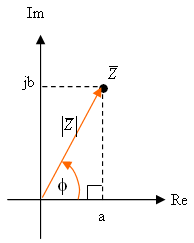
איור 10.41 

מעבר מצורה קרטזית לצורה פולארית 

בצורה קרטזית נתונים הערך הממשי a והערך הדמיוני b. לשם מציאת הגודל של המספר המרוכב בייצוג הפולארי, ,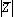

נדמה את a,b לשני ניצבים a ו- b במשולש ישר זווית. הצגת המספר המרוכב בצורה פולארית פירושה מציאת היתר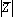  

והזווית .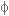

ניעזר במשפט פיתגורס למציאת היתר:

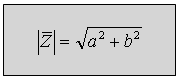
(10.17)

ניעזר בקשר הטריגונומטרי tan למציאת הזווית:

הערה: a, b יכולים להיות גם שליליים. אז נקבל זווית שלילית או זווית גדולה מ- 90⁰.

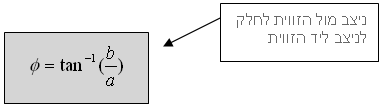
מעבר מצורה פולארית לצורה קרטזית

בצורה פולארית נתונים הגודל 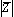 והזווית 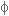. הצגת המספר המרוכב בצורה קרטזית פירושה מציאת הערכים a ו- b שלו.

נוכל להיעזר בקשרים הטריגונומטריים המוכרים במשולש ישר זווית.

הערה: הזווית 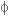 יכולה להיות גם שלילית.

ניעזר בקשרים הטריגונומטריים sin ו- cos למציאת הניצבים במשולש:

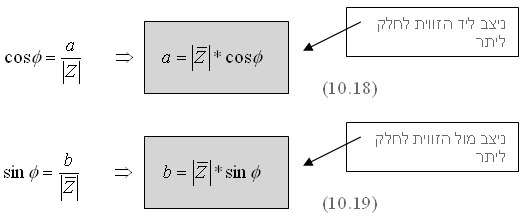
הערה: אפשר לעבור מצורה אחת לאחרת ולהפך באופן מקוצר באמצעות שימוש במחשבון.

להסבר על שימוש במחשבון לחצו כאן

אתם נדרשים להיעזר במחשבון ולאמת את תוצאות ההמרה שביצעתם בדרך טריגונומטרית בתת סעיף זה.

•   הקודם                                                                                                                             
• המשך