(The complex number)
מספר המורכב גם מערך ממשי וגם מערך דמיוני מוגדר כמספר מרוכב
(קומפלקסי) והוא ניתן גם להצגה במערכת צירים מרוכבת המכילה שני צירים: אופקי - ציר
מספרים ממשיים וציר מספרים אנכי - ציר מספרים דמיוניים כמתואר באיור 10.37.
בדוגמה הבאה יש שלוש נקודות שונות זו מזו: האחת ממשית, השנייה
דמיונית והשלישית מרוכבת.
הצגת המספר המרוכב
את המספר המרוכב אפשר להציג בכמה צורות (יש יותר מ- 2) נציג כאן
שתי צורות: הצורה הקרטזית והצורה הפולארית (קוטבית).
בצורה הקרטזית המספר המרוכב מכיל חלק
ממשי וחלק דמיוני מן הצורה הזאת:
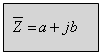
כאשר:
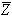 - מספר מרוכב
- מספר מרוכב
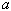
-
חלק ממשי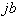 - חלק דמיוני
- חלק דמיוני
כלומר, כדי לתאר במרחב מספר מרוכב בצורה קרטזית עלינו לציין את
מיקומו על פני הציר הממשי ואת מיקומו על פני הציר הדמיוני (בדומה לציון ערכי (x,y) של נקודה במישור xy).
צורת ההצגה הקרטזית נוחה במיוחד כשצריכים לחבר או לחסר מספרים
מרוכבים. כמו כן יש יתרון לצורת ההצגה הזאת ביישומים גאומטריים.
בצורה הפולארית המספר המרוכב הוא וקטור (עם גודל וזווית) שראשיתו בראשית הצירים
וראשו בנקודה x,y, מן הצורה הזאת:
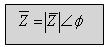
כאשר:
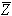 - מספר מרוכב
- מספר מרוכב
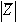 - גודל וקטורי (אורכו של
הווקטור מקדקוד מערכת הצירים ועד הנקודה שממוקמת במערכת הצירים המרוכבת)
- גודל וקטורי (אורכו של
הווקטור מקדקוד מערכת הצירים ועד הנקודה שממוקמת במערכת הצירים המרוכבת)
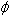 - הזווית
מציר המספרים הממשיים החיוביים ועד הווקטור עצמו. כשהזווית חיובית פירושה תנועה
נגד כיוון השעון מציר המספרים הממשיים החיוביים ועד הווקטור. זווית שלילית פירושה
תנועה עם כיוון השעון מציר המספרים הממשיים החיוביים ועד הווקטור.
- הזווית
מציר המספרים הממשיים החיוביים ועד הווקטור עצמו. כשהזווית חיובית פירושה תנועה
נגד כיוון השעון מציר המספרים הממשיים החיוביים ועד הווקטור. זווית שלילית פירושה
תנועה עם כיוון השעון מציר המספרים הממשיים החיוביים ועד הווקטור.
למשל המספר המרוכב 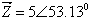 ניתן להצגה בצורה פולארית
באיור 10.38:
ניתן להצגה בצורה פולארית
באיור 10.38:
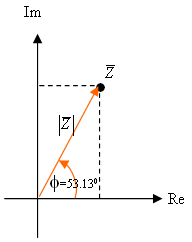
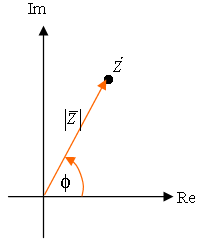
איור 10.38
את הנקודה 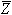 אפשר לתאר בצורה הפולארית
באמצעות זווית
אפשר לתאר בצורה הפולארית
באמצעות זווית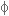 מציר המספרים הממשיים ועצמה
באורך
מציר המספרים הממשיים ועצמה
באורך 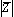 .
.
לסיכום, אפשר לתאר כל מספר
מרוכב 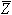 או בצורה קרטזית, על ידי
מיקומו על הציר הממשי והציר הדמיוני, או בצורה פולארית (קוטבית), על
ידי אורך
או בצורה קרטזית, על ידי
מיקומו על הציר הממשי והציר הדמיוני, או בצורה פולארית (קוטבית), על
ידי אורך 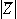 (גודל וקטורי)
וזווית
(גודל וקטורי)
וזווית מציר המספרים הממשיים.
מציר המספרים הממשיים.
לצורת ההצגה הפולארית יש יתרונות כשרוצים להכפיל או לחלק מספרים
מרוכבים.
הצגת אותות סינוס בעלי מופע השונה מאפס אינה מתאפשרת על גבי מערכת
צירים אחת ממשית, אלא ההצגה מתבצעת על פני שני צירים: ציר מספרים ממשי וציר מספרי מדומים.
מערכת צירים המשלבת ציר מספרים ממשיים וציר מספרים מדומים קרויה
מערכת צירים מרוכבת
(קומפלקסים) והיא הכרחית
בפתרון של רשתות המכילים אותות סינוס בעלי מופעים שונים.
צורת הצגה ייחודית לתורת החשמל היא צורת ההצגה הפאזורית.
למעשה, זהו מקרה פרטי של צורת ההצגה הפולארית המתאימה ליישומים בתורת החשמל.
פאזור
כל המתחים והזרמים הנמדדים באותו מעגל חשמלי לזרם חילופין,הם בעלי
אותה התדירות. לכן אין צורך להכליל את המשתנה הזה (תדירות) בתיאור המתחים והזרמים
המחושבים במעגל. אפשר להסתפק רק בערכים השונים זה מזה, שהם: התנופה (אמפליטודה)
וזווית המופע. תיאור שכולל את התנופה ואת זווית המופע קרוי תיאור פאזורי. להבהרת
הנושא נתבונן באיור 10.39.
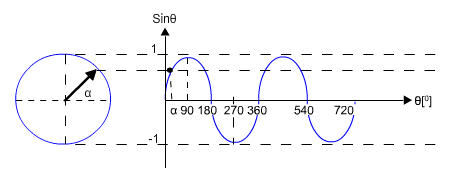
איור 10.39
כל נקודה על גרף הסינוס ניתנת לתיאור כנקודה במישור המרוכב כך שהאמפליטודה
מיוצגת על ידי רדיוס המעגל, והזווית (פאזה - מכאן השם פאזור) מיוצגת על ידי
הזווית של המחוג במישור המרוכב, ביחס לציר האופקי (באיור 10.39 הרדיוס הוא 1
והזוית היא α).
באיור 10.40 מוצגים שני אותות בעלי תנופה שונה ועם הפרש פאזה Φ ביניהם, הן במישור הזווית וגם במישור המרוכב. 1V, 2V מתוארים כשני מחוגים עם הפרש זווית Φ ביניהם.
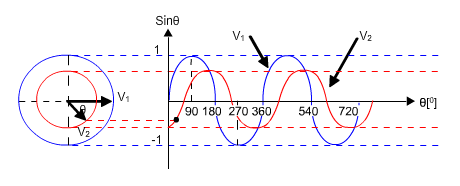
איור 10.40