קורס בתורת החשמל מאת יוסי יאשי

(Complex numbers)

את המספרים שאנו עובדים אתם אפשר לסווג לכמה קבוצות:

א. קבוצת המספרים הטבעיים (1, 2, 3,...) את הקבוצה הזאת מקובל לסמן באות N. המספרים האלה נתנו לנו את היכולת לספור עצמים. יכולנו לחבר מספרים כמו: 16 +17 = 33 (כל המספרים הם טבעיים).

ב. קבוצת המספרים השלמים התקבלה כתוצאה מקושי בפעולת החיסור, למשל:  12 - 14 = (-2). המספר

(- 2) אינו מספר טבעי. לכן הוספנו את המספרים השליליים ואת 0 שהם משתייכים לקבוצת המספרים השלמים.

ג. קבוצת המספרים השלמים אינה מספקת דיה כדי לבצע את פעולת החילוק. למשל: 2/5 = 0.4 לכן הורחבה קבוצת המספרים השלמים לקבוצת המספרים הרציונאליים (אלו מספרים מן הסוגq=m/n כאשר m, n מספרים שלמים) המסומנת באות Q.

ד. הרחבה נוספת של קבוצת המספרים נדרשה כדי להציג מספרים מן הסוג של 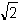. כך התקבל תחום המספרים הממשיים, המסומן באות R (מהמילה Real).

את כל אותם גדלים פיסיקליים שעבדנו אתם עד עתה אפשר להציג גם על גבי מערכת צירים המכילה מספרים ממשיים בלבד.

למשל נציג ציר של מספרים ממשיים המתאר מתח חשמלי:

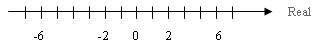
שאלה:

האם אפשר לפתור את המשוואה X²+1=0 בעזרת המספרים הממשיים בלבד?

מובן שלא. הפתרון של משוואה זאת הוא 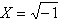תחום המספרים הממשיים אינו מכיל את .

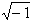אנו נדרשים להרחיב שוב את תחום המספרים המוכר לנו, כדי לפתור בעיות שבהן הפתרון הוא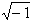 

לצורך זה נגדיר מספר חדש. המתמטיקאים מסמנים אותו באות i. אך בהנדסת חשמל שמורה האות i לסימון זרם חשמלי. לכן נסמן את המספר החדש באות j.

כלומר: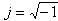 

מעוניינים לדעת קצת יותר על ההיסטוריה של המספר הדמיוני - לחצו כאן

כדי להבחין בין מספר ממשי למספר דמיוני ננסה לפתור את שני הביטויים האלה:

1. חשבו את ערכו של הביטוי המתמטי:

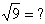
בעבר התנגדו מתמטיקאים רבים להכללת המספר החדש בתחום המספרים וקראו לו 'מספר דמיוני'. המתמטיקאי אוילר (1707 – 1783) הוא שהציע להציג מספרים אלו כנקודות במישור והראה שימושים רבים למספרים החדשים. גם המתמטיקאי גאוס (1777 – 1855) הרבה להשתמש במספרים החדשים וקרא להם בשם 'מספרים מרוכבים' (Complex Numbers). כיום תופסים המספרים המרוכבים מקום של כבוד במתמטיקה ואפשר למצוא להם שימושים גם בתורת החשמל. את תחום המספרים המרוכבים המתארים נקודות במישור, שקרוי 'המישור המרוכב', מסמנים באות C.

ברור לנו שהתשובה שמתקבלת היא 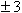 (באמצעות המחשבון נקבל את התשובה 3 בלבד).

לביטוי 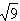 יש תשובה מספרית ממשית שניתנת גם להצגה על גבי ציר המספרים הממשיים

2. חשבו את ערכו של הביטוי המתמטי:

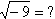
תשובה לביטוי זה אינה פשוטה וגם שימוש במחשבון לא יועיל, מכיוון שתתקבל הודעת שגיאה. הסיבה לכך היא שתוצאת ביטוי זה (שורש שלילי) היא לא מספר ממשי אלא מספר דמיוני.

נחזור לביטוי שהוצג בשאלה 2 ונוכל כבר לתת תשובה מספרית ואף להציגה על גבי מערכת צירים של מספרים דמיוניים.

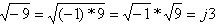
המשמעות הגרפית של הכפלת המספר 3 ב j:

אם נסמן את המספר 3 באמצעות חץ שראשיתו באפס וסופו במספר 3 על פני ציר המספרים הממשיים, הכפלה ב- j פירושה סיבוב החץ בזווית של 90⁰ שמאלה. המספר j3 מתואר על הציר האנכי.

את המספר j3 כמו מספרים דמיוניים אחרים אפשר כאמור להציג על גבי מערכת צירים במישור. המספרים הדמיוניים מוצגים על פני הציר האנכי, ואילו המספרים הממשיים מוצגים על פני הציר האופקי.

נציב את המספר הממשי 3 על גבי מערכת הצירים. כשנכפול מספר זה בפרמטר j נקבל את התוצאה j3. מבחינת גרפית אפשר לומר שבוצעה תזוזה של 90° נגד כיוון השעון ולכן קיבלנו את הערך j3 (כמתואר באיור 10.35).

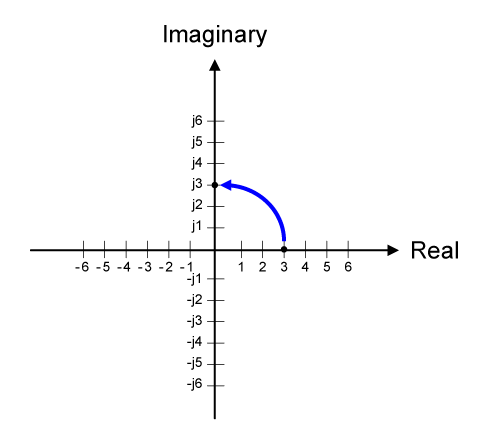
איור 10.35

ניקח את המספר הדמיוני j3 ונכפול אותו שוב ב- j. התוצאה שתתקבל תהיה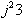 

אך מבחינה גרפית הכפלה נוספת ב- j פירושה תזוזה נוספת של 90° נגד כיוון השעון. תנועה זו תציב אותנו בנקודה -3 שעל ציר המספרים הממשיים (כמתואר באיור 10.36).

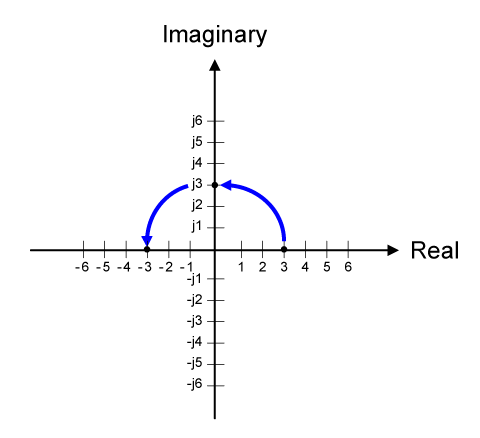
איור 10.36

אם 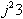שווה ל - 3 הרי שמכאן נובע ש-  

•   הקודם                                                                                                                            
•  המשך