(Sinusoidal cyclic signals)
אות מחזורי סינוסואידלי הוא דוגמה לאות חילופין. האות הזה נפוץ
מאוד ולכן כשמציינים אות AC הכוונה
היא לאות סינוס מחזורי.
הערה: המתמטיקאי והמהנדס הצרפתי פורייה הוכיח שכל אות מחזורי (לא
חשוב מהי צורתו) מורכב מטור אינסופי של אותות סינוס בעצמות שונות ובתדרים שונים.
לאות הסינוס חשיבות רבה בתחום החשמל ובשל יתרונותיו הרבים והקלות
שבייצור אות סינוסואידאלי, חברת החשמל מספקת לנו מתח סינוסואידלי.
בשל חשיבות פונקציית הסינוס נסביר תחילה את התנהגות הפונקציה כתלות
בזווית. בהמשך נעסוק בזווית שמשתנה בזמן ובעקבות כך גם פונקציית הסינוס משתנה
כתלות בזמן. לבסוף, נדון גם במושג זווית
מופע.
על פונקציית סינוס למדנו בשיעורי הטריגונומטריה. למדנו שסינוס הוא
היחס שבין הניצב שמול הזווית לבין היתר במשולש ישר זווית. ההגדרה הזאת מתאימה
לזוויות שבין 00 לבין 900.
אפשר להרחיב את הגדרת הסינוס גם לזוויות עד 3600
אם מתייחסים למעגל. במקרה כזה נגדיר סינוס כיחס שבין h לבין רדיוס המעגל, כמתואר באיור 10.15. בהגדרה החדשה הסינוס יכול
להיות גם חיובי וגם שלילי.
בצד ימין של איור 10.15 מוצגת הרחבה נוספת של פונקציית הסינוס.
הפעם מתייחסים לזוויות בגודל כלשהו (יותר מ- 3600) במקרה כזה נוח להציג
את הפונקציה כאות המשתנה באופן מחזורי. שימו לב שמחזור ההשתנות אחד נמשך 3600
כמו סיבוב אחד של המחוג במעגל שמשמאל.
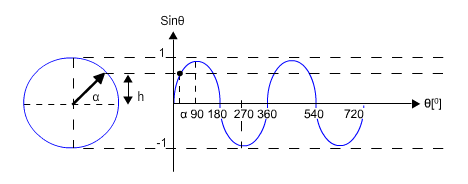
איור 10.15
כעת ניזכר בפרק 9 שבו תואר
מבנה מחולל הסינוס ועקרון פעולתו.המתח הסינוסואידלי נוצר כתוצאה מכך שכריכה נושאת
זרם הסתובבה בתוך שדה מגנטי. בכל רגע מצויה הכריכה בזווית אחרת, כלומר הזווית היא
פונקציה של הזמן (t)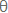
אם נסמן ב-ω את המהירות הזוויתית של הכריכה (כלומר כמה רדיאנים הכריכה עוברת
בשניה אחת), נוכל להגיד כי:
θ(t) = ωt
כעת נניח שברגע t = 0 הזווית
ההתחלתית היא אפס ונוכל לבטא את המתח כפונקציה של הזמן באמצעות ביטוי מתמטי שהובא
בפרק 9 ומובא שוב בנוסחה 10.8 לנוחות הקורא:
הביטוי הכללי של אות סינוסואידלי:
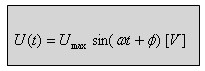
(10.8)
כאשר:
(U(t - המתח ברגע t מסוים [v]
Umax - תנופת האות (ערכו המרבי - נקרא גם אמפליטודה [v]
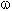 - תדירות זוויתית [rad/sec]
- תדירות זוויתית [rad/sec]
התדר הזוויתי 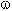 מתאר את מהירותה הזוויתית
של הכריכה, במחולל אות הסינוס, שנעה על ציר סיבובי. המהירות הזאת נמדדת ביחידות של
זווית לזמן. נזכיר שסיבוב שלם שהכריכה מבצעת (360°) פירושו שינוי זוויתי של
מתאר את מהירותה הזוויתית
של הכריכה, במחולל אות הסינוס, שנעה על ציר סיבובי. המהירות הזאת נמדדת ביחידות של
זווית לזמן. נזכיר שסיבוב שלם שהכריכה מבצעת (360°) פירושו שינוי זוויתי של 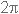 רדיאנים. עצמת אות הסינוס תלויה במצבה של הכריכה במחולל, כלומר
לזווית שבה היא מצויה ביחס לציר האנכי.. בכל סיבוב שלם שהכריכה מבצעת, מופק מחזור
שלם של אות סינוס.
רדיאנים. עצמת אות הסינוס תלויה במצבה של הכריכה במחולל, כלומר
לזווית שבה היא מצויה ביחס לציר האנכי.. בכל סיבוב שלם שהכריכה מבצעת, מופק מחזור
שלם של אות סינוס.
התיאור הגרפי של אות מתח סינוסואידאלי מובא באיור 10.16
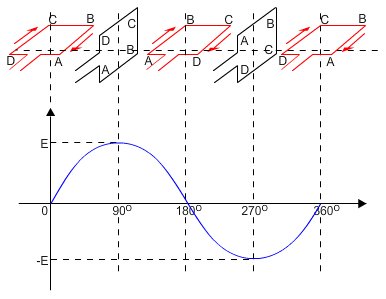
איור 10.16
התדר הזוויתי 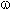 מתקבל על ידי מכפלת מספר
הפעמים שהכריכה מסתובבת בשנייה, f, ב
מתקבל על ידי מכפלת מספר
הפעמים שהכריכה מסתובבת בשנייה, f, ב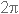 רדיאנים :
רדיאנים :
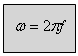
(10.9)
הערה: כדי לחשב את ערכו הרגעי של המתח, יש לבצע את החישוב כשהמחשבון
במצב rad.
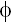 - זווית המופע של אות המתח הסינוסואידלי [ב ° או ב rad], היא הזווית ברגע ההתחלה של האות
- זווית המופע של אות המתח הסינוסואידלי [ב ° או ב rad], היא הזווית ברגע ההתחלה של האות
(כאשר t = 0). אם מדובר במתח שמייצר מחולל, אפשר לחשוב
על הזווית שבה מצויה הכריכה כשהמחולל מתחיל להסתובב.
כשמדובר באות סינוס יחיד, בדרך כל אין חשיבות רבה לזווית ברגע
ההתחלה. אולם כשמתארים בצורה גרפית שני אותות סינוס כתלות בזמן, על גבי אותו ציר
זמן. מקובל לסמן את אחד מהם כאות המתחיל בזמן אפס, ואילו לאות האחר תיתכן תזוזה
ביחס לאות המתחיל באפס בציר הזמן (תזוזה היכולה להיגרם גם מרכיבים המחוברים
למעגל - כפי שנלמד בהמשך). זווית
המופע היא אותה תזוזה של האות האחד ביחס לאות אחר.
הערה: לזווית מופע יש משמעות רק כשמדובר באות סינוס.
אם כך, בהשוואה שבין שני האותות, יכולים להיות שלושה סוגי מופעים:
אות בעל מופע
אפס 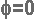
בהשוואה לאות הייחוס (אות הייחוס Uref בעל זווית מופע השווה לאפס) אין תזוזה של האות הנבדק על גבי ציר הזמן,
כלומר האות U1 התחיל להופיע מזווית 0.
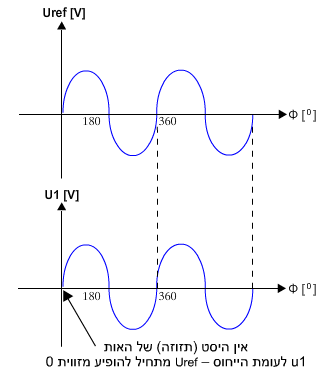
איור 10.17
אות בעל מופע
חיובי 
השוואה לאות הייחוס (אות
הייחוס Uref בעל זווית מופע השווה לאפס) יש תזוזה של האות הנבדק על גבי ציר הזמן
נגד כיוון הציר (שמאלה). זווית המופע של האות U2 היא 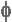 + כפי שמתואר באיור 10.18
+ כפי שמתואר באיור 10.18
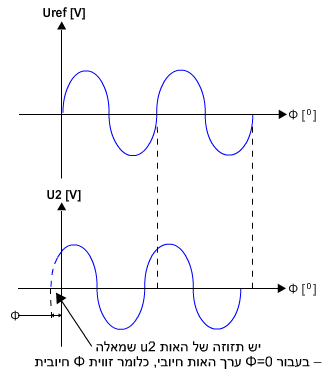
איור 10.18
אות בעל מופע
שלילי 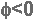
בהשוואה לאות הייחוס (אות
הייחוס Uref בעל זווית מופע השווה לאפס) יש תזוזה של האות הנבדק על גבי ציר הזמן
עם כיוון הציר (ימינה). זווית המופע של האות U3 היא 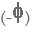 כמתואר באיור 10.19.
כמתואר באיור 10.19.
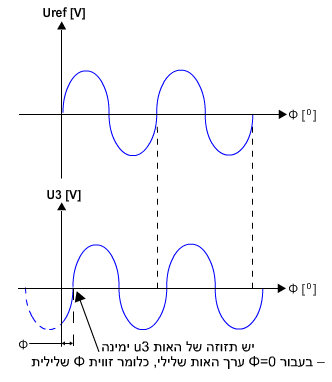
איור 10.19
הערה:
אות בעל מופע של 180° זהה בדיוק לאות בעל מופע של 180°-.אפשר
לראות את האותות האלה באיור 10.20:
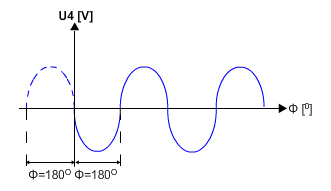
איור 10.20