קורס בתורת החשמל מאת יוסי יאשי

(Basic concepts of cyclic signals)

יש כמה מושגי יסוד שעלינו להכיר, הקשורים בעבודה עם אותות מחזוריים - אותות שצורת ההשתנות שלהם חוזרת על עצמה בכל פרק זמן קבוע.

א. זמן מחזור (period) - מוגדר כאותו פרק זמן העובר מרגע שהאות מצוי בנקודה כלשהי של מחזור אחד עד שהאות מגיע שוב לאותה הנקודה במחזור הבא, כפי שאפשר לראות באיור 10.5. את זמן המחזור מודדים ביחידות של שניות [sec].

נתון אות חשמלי כמתואר באיור 10.5:

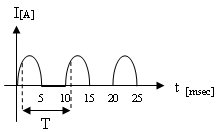
איור 10.5

את זמן המחזור של האות אפשר לחשב בכמה דרכים:

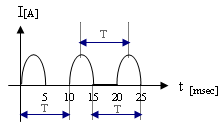
ב. תדר האות (frequency) - מוגדר כמספר המחזורים בשנייה אחת.

את תדר האות מודדים ביחידות [1/sec] או [Hz] הרץ.    

רוצים לדעת מי היה הרץ? לחצו כאן       

את התדר אפשר לחשב אפוא באופן הזה ("כמה מחזורים נכנסים בשנייה אחת"):

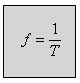
(10.1)

כאשר:

f - תדר האות  [Hz]

T - זמן המחזור [sec]

נתון אות חשמלי כמתואר באיור 10.6:

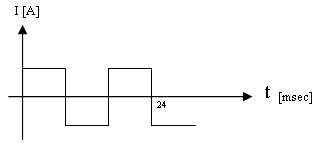
איור 10.6

ג. תנופת האות (משרעת הגל) - הערך המרבי שאליו יכול האות להגיע. נמדד ביחידותיו של אותו גודל פיסיקלי נבדק (מתח, זרם, או הספק) ומסומן באמצעות האינדקס max.

נתון אות חשמלי כמתואר באיור 10.7:

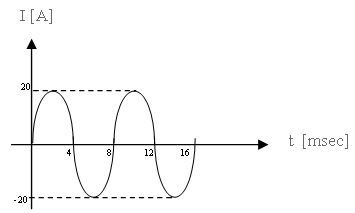
איור 10.7 

כלומר תנופת האות היא:

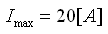
ד. ערך משיא לשיא - מוגדר כאותו הפרש בין ערכו המרבי של האות לערכו המזערי של האות ומסומן באינדקס

(p-p (peak to peak.

הערה: באותות סינוס הערך משיא לשיא מוגדר גם כפעמיים תנופת הגל.

נתון אות חשמלי כמתואר באיור 10.8:

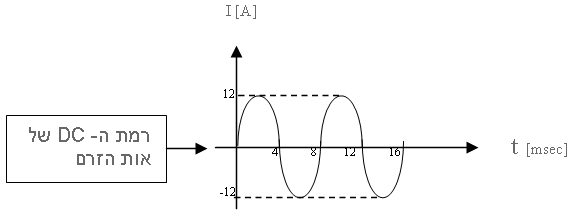
איור 10.8 

כלומר:

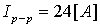
ה. ערכו הממוצע של האות המחזורי - מחושב בעבור מחזור אחד לפי השטח הכלוא בין גרף הפונקציה לבין ציר הזמן (t) . לצורך זה נתייחס לשטח שמעל ציר הזמן כשטח חיובי ולשטח מתחת לציר הזמן כשטח שלילי. הערך הממוצע נמדד ביחידותיו של אותו גודל פיסיקלי נבדק ומסומן באמצעות האינדקס av.

אפשר לחשב את הערך הממוצע של האות כמתואר בנוסחה 10.2:

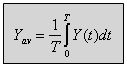
(10.2)

כאשר:

Yav - ערכו הממוצע של הגודל הפיסיקלי Y

(Y(t - פונקצית הגודל הפיסיקלי כתלות בזמן (עבור מחזור בודד)

T - זמן המחזור של האות [Y [sec

הערה: הערך הממוצע של האות מתאר למעשה את ערך ה- DC של אותו האות (רמה אופקית שמהווה את הציר עליו רוכב הגל - ראו איור 10.8).

לכן בעבור אותות סינוס הערך הממוצע הוא תמיד אפס כי רמת ה- DC של אותות אלה הוא גם כן אפס.

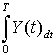 - זהו "השטח הכלוא באותו מחזור". לכן בעבור אות סינוס ערך זה שווה אפס

(שטח הסינוס העליון החיובי שווה לשטחו התחתון השלילי) ומתקבל גם שערכו הממוצע של האות מתאפס.

נתון אות חשמלי כמתואר באיור 10.9:

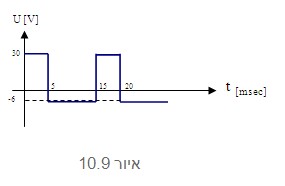
נתמקד באותם שטחים שכלואים באותו זמן מחזור כפי שמובא באיור 10.10 ונחשב את ערכו הממוצע של אות המתח הנתון בשתי דרכים:

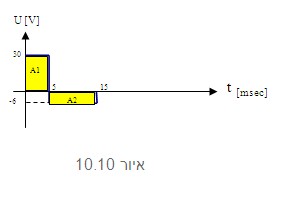
1. נחשב את השטחים הכלואים במחזור ונחלק בזמן המחזור כולו למציאת ערכו הממוצע של האות:

2. נחשב את ערכו הממוצע של אות המתח על פי ההגדרה המתמטית 10.2:

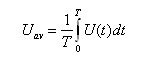
אפשר לראות באיור 10.10 שבזמן מחזור אחד קיימות שתי פונקציות של מתח:

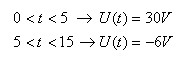
נרשום את ההגדרה המתמטית לחישוב ערכו הממוצע של אות המתח: 

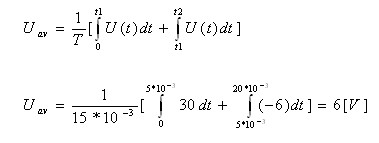
ו. יחס המחזור

Duty Cycle - היחס שבין משך זמן הדופק החיובי של האות לבין משך זמן המחזור כולו. מקובל למדוד את  היחס הזה באחוזים.

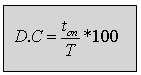
(10.3)

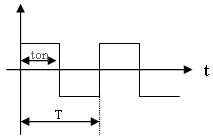
איור 10.11 

נתון אות מחזורי ריבועי בתדר של kHz1 בעל יחס מחזור של 40%.

ז. ערך יעיל (אפקטיבי) של האות המחזורי - מוגדר כאותו מתח שווה ערך DC שאם נחברו במקום אות ה- AC הקיים, הספק הצרכן לא ישתנה. הערך היעיל נמדד באותן יחידות של  הגודל הפיסיקלי הנבדק ומסומן באמצעות האינדקס eff, או ב rms. המשמעות של ראשי התיבות rms תובהר בהמשך בעזרת  ההגדרה המתמטית של גודל זה.

כדי להבין את המושג הזה (אחד מן המושגים החשובים ביותר ב- AC) נתבונן בדוגמה הזאת:

מחברים את אות המתח הבא לנורת ליבון כמתואר באיור 10.12

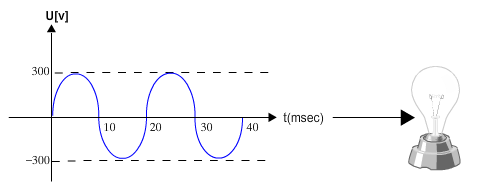
איור 10.12

כתוצאה מחיבורה למקור מתח זה, נדלקה הנורה וצרכה הספק של 75W.

חיבור אותה נורה למקור מתח ישר DC תגרום גם כן להדלקתה.  נשאלת אפוא השאלה: מה ערכו של מתח ה DC שיגרום למנורה להאיר באותה העצמה? התשובה היא: ערך מתח ה- DC שיחובר לאותה מנורה ויגרום להדלקתה באותה עצמת הארה ובאותו הספק (של 75w) כפי שפעלה קודם לכן, כשהייתה מחוברת למקור ה-AC, שווה לערך היעיל של אות מתח הסינוס.

 הערות:

1.     את  הערך היעיל בחרנו להשוות לערך DC, בעיקר מטעמים דידקטיים, אך אין משמעות הדבר שלכל צרכן הפועל בזרם חילופין אפשר להחליף את מקור החילופין, המפעיל אותו, במקור מתח DC אחר, משום שיש צרכנים שפועלים רק במתח חילופין.

2.     אם נחבר מד מתח AC למקור מתח חילופין נקבל על צג המכשיר מספר קבוע. על אף שהאות הנבדק הוא סינוס למשל, וערכיו משתנים בכל רגע נתון, מד המתח הראה מספר קבוע. מספר זה שהוצג על ידי מד המתח הוא בעצם ערכו היעיל של האות הנבדק!

את חישוב הערך היעיל (אפקטיבי) של כל אות מחזורי אפשר לבצע על ידי חישוב השורש של ממוצע הריבועיים (Root Mean Square) של מחזור

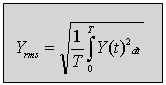
(10.4)

כאשר:

Yrms - ערכו היעיל של הגודל הפיסיקלי Y

Y(t)² - ריבוע פונקצית הגודל הפיסיקלי (עבור מחזור בודד)

T - זמן המחזור של האות sec] Y]

הערה: אם נבדוק בעבור אות סינוס מהו ערכו היעיל נגלה שהוא פונקציה של תנופת האות בלבד!

אפשר לחשב ערך יעיל RMS של אותות סינוס בלבד ולהראות ש:

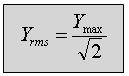
(10.5) 

כאשר:

Ymax - תנופת האות (משרעת הגל)

•   הקודם                                                                                                                             
• המשך