קורס בתורת החשמל מאת יוסי יאשי

(The relationship between voltage and current in a capacitor)

כפי שלמדנו קודם לכן, הקשר בין מתח ובין מטען בקבל הוא:

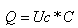
אם נבצע גזירה לפי t על שני האגפים, נקבל את הקשר בין המתח ובין הזרם בקבל:

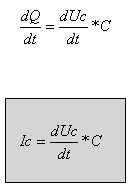
7.23

מנוסחה 7.23  אפשר לראות שהזרם בקבל יחסי לקצב שינוי המתח על פני הקבל ותלוי גם בגודל הקבל עצמו.

הערה: חשוב לציין שעד עתה לא התייחסנו לזרם בקבל מכיוון שהטענה הייתה שבקבל טעון מצטבר מטען ולא עובר בו זרם. אמנם בקבל טעון לא עובר זרם, אבל עד לרגע שהוא נטען קיים זרם במעגל, שאותו אפשר לחשב באמצעות משוואה 7.23. עוד יש לציין שדרך הקבל עצמו מעולם לא זורם זרם, בטעינת הקבל קיים מעבר של מטענים דרך המוליכים במעגל, כלומר יש זרם במעגל שאינו חוצה את הבידוד הדיאלקטרי שבין הלוחות. כשאנו אומרים שדרך הקבל עובר זרם, אנו מתכוונים לזרם במעגל.

כאשר : קצב שינוי המתח הוא 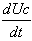 לביטוי זה קוראים גם נגזרת המתח על הקבל לפי הזמן t

דוגמה:

נתון קבל שמחובר למקור מתח ישר של V50 כמתואר באיור שלפניכם:

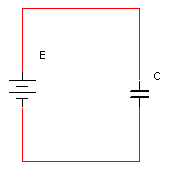
ממשוואה 7.23  אפשר להסיק שרק כשיש שינוי של מתח בקבל יזרום דרכו זרם. זו הסיבה לכך שקבל המחובר למקור מתח- DC מהווה נתק, אחרי שהסתיימה טעינתו.

בהזדמנות זאת נציין גם שהקבל הוא רכיב שמתנגד לשינויי מתח.

המתח על הקבל

נרשום את משווה 7.23 ונחלץ את המתח על הקבל ממשוואה זו:

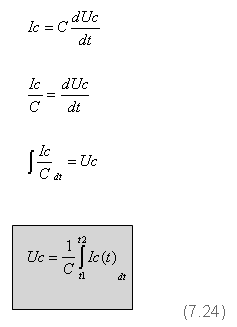
מנוסחה 7.24 אפשר להסיק שכאשר בקבל עובר זרם (ולא משנה מה צורתו ועצמתו) יש עליו מתח שמשתנה (המתח יכול גם לקטון) ככל שהזמן t עובר.

•   הקודם                                                                                                                             
• המשך