קורס בתורת החשמל מאת יוסי יאשי

(Series connection of capacitors)

בחיבור קבלים בטור אין נקודות צומת ביניהם. טעינת לוחות הקבלים המחוברים בטור מתבצעת באמצעות השראה אלקטרוסטטית.

דוגמה למעגל טורי של שלושה קבלים:

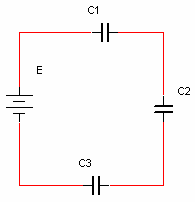
איור 7.35

תכונות המעגל הטורי

כדי לקבוע את תכונות המעגל הטורי נתבונן במעגל שבאיור 7.36:

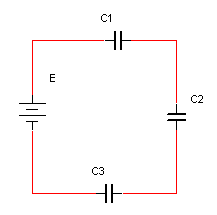
תכונה ראשונה

המטען בכל קבל שווה וזהה גם למטען הכללי.

כדי להבין את התכונה הזאת נאמר שעם חיבור המעגל למקור המתח הלוחות השמאליים של הקבלים C1 ו- C3 נטענו מיד באמצעות מקור המתח ל- +Q ו-  -Q. הלוחות הימניים של כל אחד מהם נטען באמצעות השראה אלקטרוסטטית למטענים שווים אך מנוגדים. מאחר שהלוח הימני של הקבל C1 נוגע באופן פיסי בלוח העליון של הקבל C2, מתבצעת הפרדת מטענים במוליך כך שהמטען בלוח העליון של C2 הנו חיובי +Q ואילו בלוח הימני של C1 יש מטען -Q. הלוח הימני של הקבל C3 נוגע בלוח התחתון של הקבל C2 ושוב ביניהם יש הפרדת מטענים כך שהלוח התחתון של הקבל C2 יהיה טעון –Q ואילו הלוח הימני של הקבל C3 במטען +Q. מכאן אפשר לומר ששלושת הקבלים טעונים באותו מטען Q.

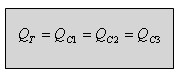
אפשר לראות שבמעגל טורי המטען מתנהג כמו הזרם מבחינת התכונה עצמה, על אף שבפועל בין הקבלים לא זורם זרם (אין תנועה של מטענים – הם במצב סטטי).

תכונה שנייה

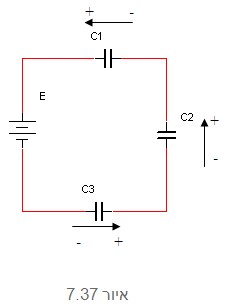
על פי חוק המתחים של קירכהוף אפשר לומר שסכום כל המתחים על פני הקבלים במעגל הטורי (בחוג הסגור) שווה למתח המקור.

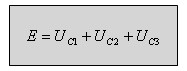
(7.18)

יש לציין שקוטביות המתח על כל אחד מן הקבלים במעגל נראית כך (בהתאם לקוטביות מטען הלוחות):

תכונה שלישית

אפשר להחליף את כל קבלי המעגל בקבל אחד שקול CT, כך שהמטען הכללי במעגל לא ישתנה.חישוב הקבל השקול CT במעגל טורי יחושב כך -

על פי חוק המתחים של קירכהוף:         

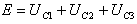
נבטא כל אחד מן המתחים על פי נוסחת המטען בקבל:

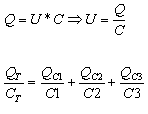
מאחר שהמטען בכל קבל שווה בחיבור טורי, אפשר לרשום זאת כך:

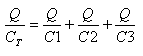
נחלק את כל המשוואה ב- 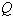, ונקבל:

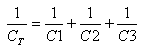
הנוסחה הזאת שהתקבלה דומה  לנוסחת חישוב התנגדות שקולה של נגדים המחוברים במקביל.

לכן קיבול שקול בטור מחושב כמו התנגדות שקולה במקביל:

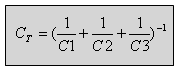
(7.19)

חיבור הקבל השקול למקור המתח

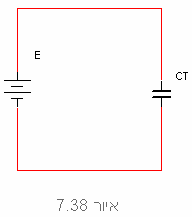
הערה:

כאשר  n מציין את מספר הקבלים הזהים שחוברו בטור.

תכונה רביעית

האנרגיה הכוללת במעגל שווה לסכום האנרגיות הנצרכות על ידי כל אחד מן הקבלים במעגל. במעגל הדוגמה שמתואר נקבל אפוא:

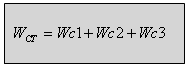
(7.20)

בחישוב אנרגיה שקולה אין חשיבות לצורת החיבור בין הקבלים!

•     הקודם                                                                                                                             
• המשך