קורס בתורת החשמל מאת יוסי יאשי

תרגיל דוגמה 16

נתון מעגל המכיל ארבעה קבלים המחוברים במקביל כמתואר באיור 7.32

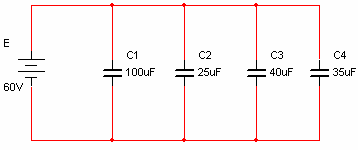
איור 7.32 

חשבו את:

א)     קיבול שקול CT;

ב)     המטען האגור בקבלים C1 ו- C3;

ג)       האנרגיה בקבל C2;

ד)      הקבל C4 הוא קבל לוחות בעל חומר דיאלקטרי יחסי  3.5=re. שטח כל לוח 40 סמ"ר. חשבו את המרחק בין לוחות הקבל.

פתרון תרגיל דוגמה 16

א. חישוב הקיבול השקול של קבלים במקביל דומה לחישוב ההתנגדות השקולה של נגדים בטור, לכן:

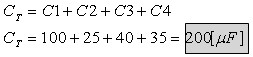
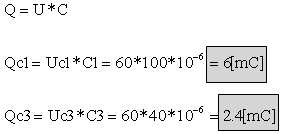
ג. חישוב אנרגיה בקבל C2

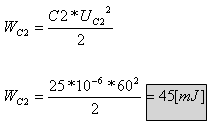
ד. נרכז את הנתונים בעבור הקבל C4:

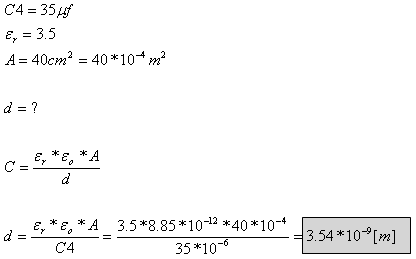
תרגיל דוגמה 17

חמישה קבלים זהים מחוברים במקביל למקור מתח ישר של 200V. האנרגיה הכללית במעגל שווה 0.2J.

חשבו:

א. את גודל כל אחד מן הקבלים;

ב. את המטען בקבל יחיד;

ג. מחברים קבל נוסף במקביל למעגל. מה יקרה למטען שחישבתם בסעיף ב?

ד. מהו גודלו של הקבל שחובר בסעיף ג, אם ידוע שהמטען הכולל במעגל השתנה ל- mC2.6?

פתרון תרגיל דוגמה 17

א. ראשית נמצא את הקבל השקול CT

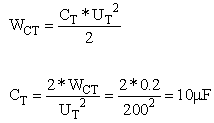
ידוע שבעבור n קבלים זהים המחוברים במקביל מתקיים:

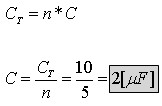
ב. נחשב מטען על כל קבל יחיד:

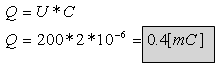
ג. חיבור קבל נוסף במקביל לא ישפיע על המטען של כל קבל יחיד, משום שהמתח במקביל נשאר ללא שינוי. כתוצאה מחיבור הקבל הזה המטען הכללי יגדל!

ד. נחשב את המטען הכללי טרם חיבור הקבל הנוסף:

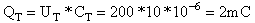
חיבור הקבל הנוסף גרם למטען הכללי לעלות ל- mC2.6. לכן ההפרש בין המטען הכללי שלאחר החיבור לבין זה שלפני החיבור, מבטא את המטען של הקבל הנוסף שחובר. לכן קיבולו של הקבל שחובר הוא:

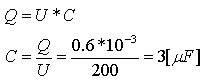
תרגיל דוגמה 18

המטען הכולל במעגל שבאיור 7.33 שווה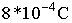 

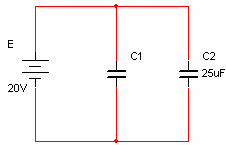
איור 7.33 

חשבו:

א. את גודל הקבל C1.

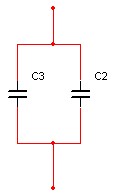
ב. מנתקים את הקבל C2 מן המעגל ומחברים אותו לקבל C3 שערכו µF20 כמתואר באיור הבא. חשבו את המתח שיופיע על הקבל C2 לאחר חיבורו לקבל C3 (יש להניח שהקבל C3 אינו טעון).

פתרון תרגיל דוגמה 18

א. נמצא תחילה את המטען בקבל C2:

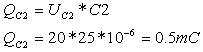
ניעזר בחוק קירכהוף:

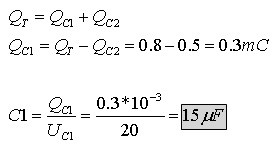
חיבור הקבל C2 לקבל C3  במקביל יגרום למטען שהיה אגור בקבל C2 להתחלק גם לקבל C3. כלומר  על פי חוק שימור מטען, המטען אינו יכול להיעלם כך סתם, אך אותו מטען שהיה בקבל ,C2 טרם חיבורו ל C3, הפך להיות המטען הכולל של שני הקבלים C2 ו- C3.

לכן חישוב המתח השקול על שני הקבלים יהיה:

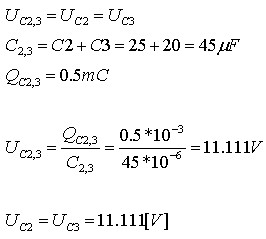
תרגיל דוגמה 19

במעגל  שבאיור 7.34 ידוע יחס הקבלים. המטען בקבל C2 שווה mC1.2.

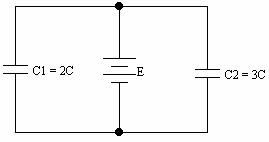
איור 7.34

חשבו את מתח המקור אם ידוע שהאנרגיה הכללית במעגל היא 0.4J.

פתרון תרגיל דוגמה 19

כפי שלמדנו בעבר, תרגילים עם יחס נגדים מומלץ לפתור באמצעות כלל מחלק הזרם או מחלק המתח.  באופן דומה נפתור גם תרגילים עם יחס קיבולים כפי שמתואר בתרגיל. בנושא זה, יש לזכור, שאת כלל מחלק המתח  יחליף כלל אחר שנקרא לו כלל מחלק המטען (לאחר טעינת הקבל, כאמור, לא זורם דרכו זרם). על פי הכלל הזה, בעבור שני קבלים המחוברים במקביל, אפשר למצוא את המטען בענף מקבילי כלשהו בדומה לחלוקת מתח בין נגדים בטור, כפי שרשום במשוואה 7.17.

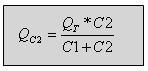
(7.17)

הערה: כלל זה גם תקף ליותר משני קבלים המחוברים במקביל (בדיוק כמו כלל מחלק המתח בנגדים).

ניעזר בכלל מחלק המטען למציאת המטען הכולל של המעגל:

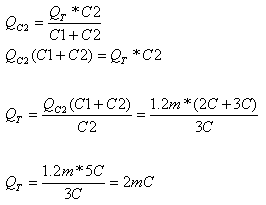
כעת אפשר למצוא את מתח המקור באמצעות נוסחת האנרגיה בקבל:

•   הקודם                                                                                                                            
•  המשך