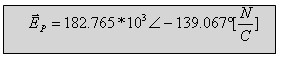קורס בתורת החשמל מאת יוסי יאשי

תרגיל דוגמה 5

נתון מטען חשמלי נקודתי כמתואר באיור 7.15:

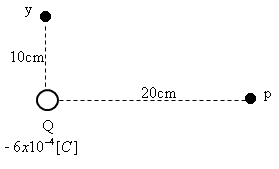
איור 7.15

חשבו את:

א.     השדה החשמלי ומגמתו בנקודותp   ו-  y

ב.     חזרו על סעיף א' בעבור מטען חיובי

פתרון תרגיל דוגמה 5

א. מאחר שהמרחקים ידועים נשתמש במשוואה 7.3 למציאת שדה חשמלי של מטען יחיד:

חשוב לזכור שאת המטען יש לרשום בערך מוחלט (תמיד חיובי) משום שגודל אינו יכול להיות שלילי.

חישוב השדה בנקודה p:

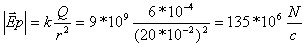
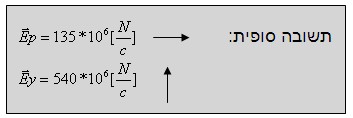
ב. קוטביות המטען אינה משפיעה על עצמת השדה בנקודות השונות, אלא רק על הכיוון. לכן:

תרגיל דוגמה 6

נתונים שני מטענים נקודתיים כמתואר באיור 7.16:

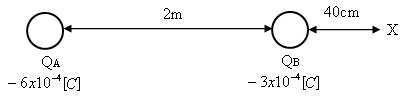
איור 7.16

חשבו את:

א.    עצמת השדה החשמלי במקום הימצאותו של המטען QA

ב.    השדה החשמלי ומגמתו בנקודה P

ג.    בין שני המטענים הנקודתיים קיימת נקודה שבה מתאפס השדה החשמלי. חשבו את המרחק והמיקום יחסית למטען QA שבו מתאפס השדה החשמלי.

פתרון תרגיל דוגמה 6

א. ניעזר במשוואת השדה החשמלי 7.3 למציאת עצמת השדה החשמלי בנקודה A:

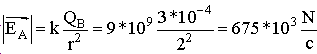
הערה: יש להבהיר שהמטען QA אינו משפיע על השדה החשמלי במקום שבו הוא מצוי. רק המטענים החיצוניים לו יוצרים שדה חשמלי במקום שבו מצוי QA.

אפשר לשים לב לכך שבפתרון הצבנו את גודל המטענים בערך מוחלט מכיוון שנדרשנו בשאלה לחשב את עצמת השדה בלבד (גודל ללא כיוון).

ב. בחישוב השדה החשמלי בנקודה P ניעזר בסכום וקטורי של שדות כל המטענים, כלומר נבחן מהי התרומה של כל מטען נקודתי לשדה בנקודה P ונסכם את כל התרומות:

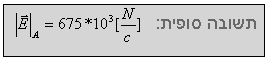
השפעת המטען QA על השדה בנקודה P:

יש לזכור שבנקודה P מציבים מטען בוחן חיובי!

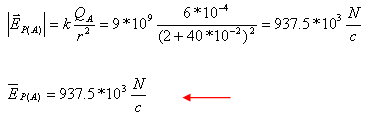
השפעת המטען QB על נקודה P:

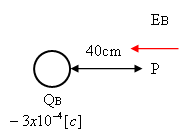
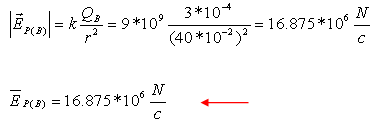
מאחר ששני השדות, שחושבו קודם לכן, באותו כיוון (שמאלה) יש לסכמם סיכום פשוט. התוצאה שתתקבל תהיה גם כן, בוודאות, עם מגמה לכיוון שמאל:

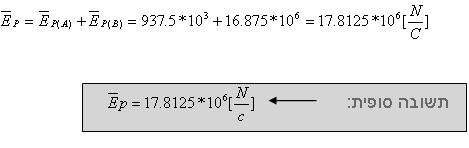
ג. מאחר ששני המטענים שווי סימן, קיימת ביניהם נקודה שבה השדה החשמלי מתאפס. הסיבה לכך היא שכל מטען מייצר שדה בכיוון הפוך וכשהשדות שנוצרים זהים בגודלם, החיבור הווקטורי ביניהם נותן אפס (כדי להגיע למסקנה זו יש להציב מטען בוחן חיובי באותה נקודה).

נגדיר נקודה y על גבי הציר שמחבר בין שני המטענים, שהיא מבטאת את המרחק מן המטען QA.

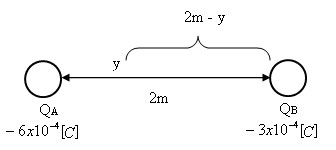
נחשב באמצעות סיכום וקטורי את השדה שנוצר בנקודה y כתוצאה מהימצאות כל אחד מן המטענים לחוד.

השפעת המטען QA על נקודה y:

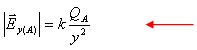
השפעת המטען QB על נקודה y: 

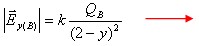
השדה השקול שמתקבל בנקודה y הוא חיבור וקטורי של כל אחד מן השדות שהתקבלו. מאחר שמגמתם הפוכה, יש לבצע חיסור בין הגדלים שהתקבלו. רק אם יהיו הגדלים הווקטורים שווים בגודלם התוצאה תתאפס.

במילים אחרות,אפשר לומר שהתנאי לאיפוס השדה החשמלי בנקודה y הוא:

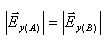
נשווה בין הביטויים כדי לחלץ את הפרמטר y המבטא את המרחק מן המטען QA (שהוא גם מה שנדרש בשאלה):

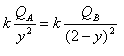
נחלק את שני אגפי המשוואה בפרמטר k ונכפול בהצלבה:

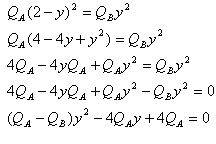
נציב מספרים ונקבל משוואה ריבועית (את המטענים יש להציב בערך מוחלט):

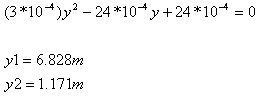
תרגיל דוגמה 7

נתונים שלושה מטענים נקודתיים כמתואר באיור 7.17:

חשבו את וקטור השדה החשמלי בנקודה P.

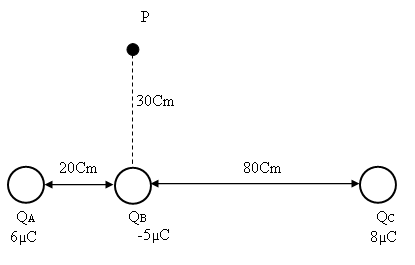
איור 7.17

פתרון תרגיל דוגמה 7

גם בתרגיל זה נבצע סיכום וקטורי  כשנבחן את השפעת אחד מן המטענים  לחוד בנקודה P.

כאמור בתרגילים אלה, יש לבנות מערכת צירים על אותה נקודה שבה דרוש למצוא את וקטור השדה החשמלי  (נקודת קדקוד מערכת הצירים תהיה בנקודה P).

נבחן כיצד משפיע כל מטען לחוד על השדה החשמלי בנקודה P.

המטענים CQ ו- AQ מפעילים כוח דחייה על מטען הבוחן שבנקודה P, ואילו המטען BQ מפעיל כוח משיכה.

נחשב תחילה את גודל כל אחד מן השדות שנוצרים על ידי כל אחד מן המטענים ורק לבסוף נרכיב בין התוצאות (נחבר וקטורית בין השדות).

השפעת המטען BQ על נקודה P (חישוב הגודל):

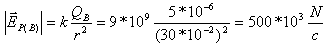
כדי לבדוק את השפעת שאר המטענים, יש לחשב את המרחק של כל אחד מן המטענים עד נקודה P. את החישוב הזה נבצע באמצעות משפט פיתגורס:

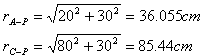
השפעת המטען AQ על נקודה P (חישוב גודל וקטורי):

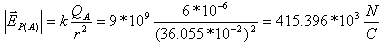
השפעת המטען CQ על נקודה P (חישוב גודל וקטורי):

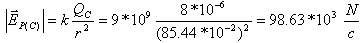
את וקטור השדה השקול בנקודה P נחשב על ידי פירוק להיטלים. כלומר נחבר לחוד את רכיבי ה- X של השדות, ובאופן דומה נחבר את רכיבי ה- Y של השדות ולבסוף נמצא את וקטור השדה השקול הקיים בנקודה P. כאמור, כדי לבצע את החישוב הזה, נבנה מערכת צירים שבה נקודה P היא נקודת הקדקוד כמתואר באיור 7.18

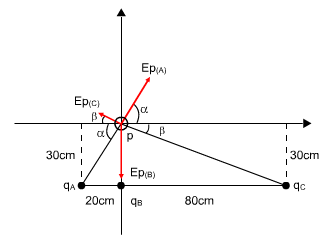
איור 7.18

כיווני וקטורי השדה הם בהתאם לכוחות שפועלים על מטען הבוחן (החיובי) שקיים בנקודה P (דחייה/משיכה).

כדי לחשב את ההיטלים השונים של כל וקטור, יש צורך לחשב את הזוויות

a ו- b. לשם כך ניעזר בתכונות משולש ישר זווית:

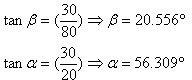
הזוויות האלה שחושבו הן הזווית של וקטורי השדה החשמלי בנקודה  P (זוויות קדקודיות) כמתואר באיור 7.18

באיור 7.19 מתואר פירוק לרכיבים אופקיים ואנכיים של רכיבי השדה החשמלי

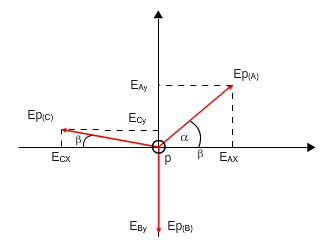
איור 7.19

אפשר לראות כי לווקטור 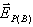 היטל ציר ה-  Xשווה לאפס, ואילו היטל ציר ה-Y שווה לגודל של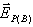 

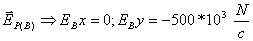
לגבי הווקטורים 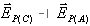פירוק ההיטלים יהיה לפי משולש ישר זווית:

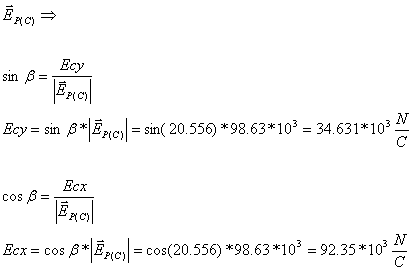
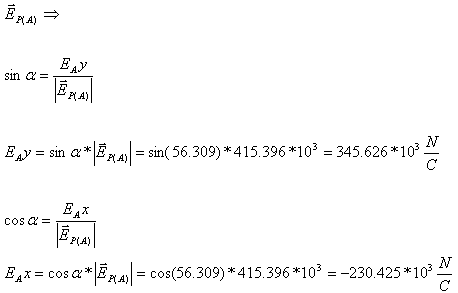
כעת נחבר בין ההיטלים השונים בהתאמה, לצורך קבלת היטלים שקולים (לכל אחד מן הצירים):

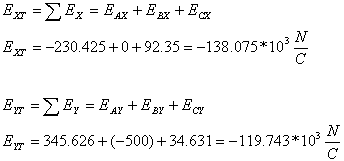
ניצור את הנקודה שהתקבלה על גבי מערכת צירים ונסרטט את וקטור השדה החשמלי הפועל בנקודה P כמתואר באיור 7.20.

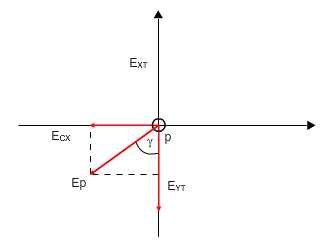
איור 7.20

באמצעות משפט פיתגורס נחשב את הגודל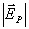 

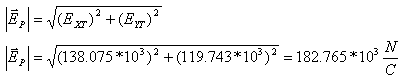
כדי למצוא את הווקטור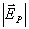 ביחס הצירים לציר ה- X החיובי, יש למצוא את הזווית g ולהוסיף לה ° 90

(מאחר שהתנועה היא לכיוון השלילי במערכת הצירים, הזווית שתחושב תהיה שלילית).

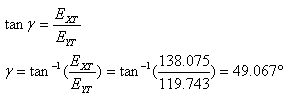
וקטור השדה החשמלי בנקודה P ביחס לראשית הצירים הוא:

•   הקודם                                                                                                                           
•   המשך