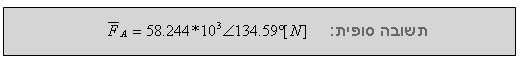קורס בתורת החשמל מאת יוסי יאשי

תרגיל דוגמה 1

נתונים שני מטענים נקודתיים כמתואר באיור 7.2. בין המטענים פועל כוח דחייה של   4[N].

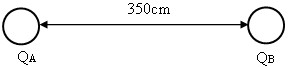
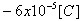
איור 7.2

חשבו את:

א.    גודלו של המטען QB

ב.     גודל הכוח בין שני המטענים אם יוכפל המרחק ביניהם.

פתרון תרגיל דוגמה 1

א. ניעזר בחוק קולון:

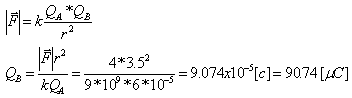
הערות:

1.     את המרחק יש לרשום במטרים.

2.     את המטען יש  לרשום בקוטביות חיובית (בערך מוחלט), כי אנו מתעניינים רק  בגודל הכוח, שהוא תמיד חיובי (גם כשמדובר בכוח משיכה).

מאחר שנתון בשאלה שבין  המטענים פועל כוח דחייה, קוטביות המטען BQ חייבת להיות שלילית!

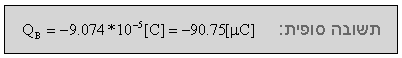
ב. אפשר לפתור את הסעיף הזה גם ללא הצבת נתונים חדשים:

אפשר לראות על פי חוק קולון, שהגדלת המרחק בין המטענים פי 2, תגרום להקטנת הכוח פי 4.

תרגיל דוגמה 2

פתרון תרגיל דוגמה 2

ניעזר בחוק קולון:

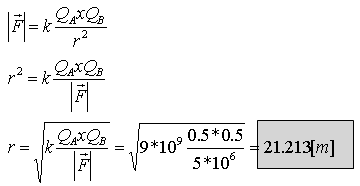
תרגיל דוגמה 3

קו ישר מחבר בין שלושה מטענים נקודתיים כמתואר באיור 7.3:

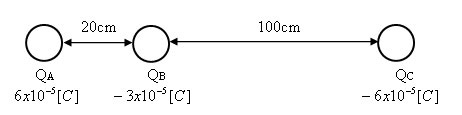
איור 7.3

חשבו את:

א.    גודל הכוח הפועל על המטען AQ ומגמתו

ב.    חזרו על סעיף א, כאשר משנים אך ורק את קוטביות המטען AQ

פיתרון תרגיל דוגמה 3

חוק קולון מסייע לנו בחישוב כוחות הפועלים בין שני מטענים. עד כה השתמשנו בחוק קולון לחישוב הכוחות הפועלים בין שני מטענים בלבד. בתרגיל זה נתונים שלושה מטענים ולכן השימוש בחוק קולון לא יהיה באופן הרגיל.

בתרגילים כאלה נבדוק בכל פעם באמצעות חוק קולון מהי התרומה של כל מטען לחוד על המטען  AQ. הכוח הפועל על AQ הוא סכום הכוחות שמפעיל כל מטען לחוד על המטען AQ. מאחר שכל המטענים מצויים על קו ישר אחד, הסכום הוא סכום פשוט. בהמשך נלמד על מקרים שבהם המטענים אינם על קו ישר אחד.

כך, בכל אחד מן החישובים נתייחס אך ורק לשני מטענים A)Q והמטען האחר).

לבסוף, נסכם את כל התוצאות שהתקבלו ונקבל את הכוח האמיתי הפועל על המטען AQ

א. נבדוק כיצד משפיע כל אחד מן המטענים על AQ 

השפעת המטען BQ על המטען AQ:

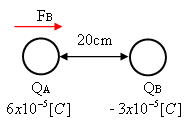
איור 7.4

הכוח שפועל בין שני המטענים במצב זה זהה, אך הפוך בקוטביות. מאחר שהמטען שמעניין אותנו בתרגיל הוא AQ, נבדוק רק את הכוח שמופעל עליו כתוצאה מן המטען BQ כוח זה ייקרא בשם BF (הכוח שמפעיל מטען BQ על מטען AQ) והוא כוח משיכה.

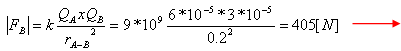
השפעת המטען cQ על המטען AQ:

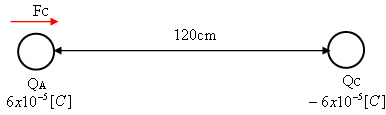
איור 7.5

הכוח שמפעיל מטען cQ על מטען AQ יקרא בשם cF והוא כוח משיכה. נחשב את הכוח הזה:

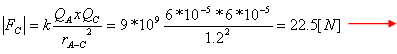
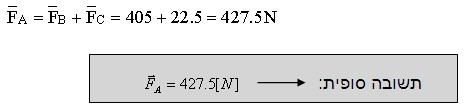
חישוב הכוח האמיתי שפועל על המטען QA  (סיכום ווקטורי של התוצאות):

מאחר ששני הכוחות חושבו קודם לכן באותו כיוון (ימינה), יש לעשות סיכום פשוט של הכוחות. התוצאה שתתקבל תהיה גם היא, בוודאות, לכיוון ימין.

ב. גודל הכוח יישאר ללא שינוי אך מגמתו תשתנה (המטענים יפעילו כוח דחייה על AQ):

תרגיל דוגמה 4

נתונים שלושה מטענים נקודתיים הממוקמים במרחב כמתואר באיור 7.6 :

חשבו את וקטור הכוח הפועל על המטען AQ.

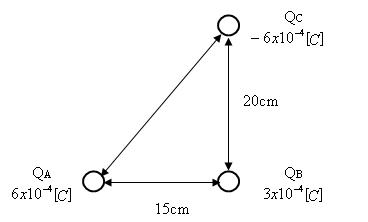
איור 7.6

פתרון תרגיל דוגמה 4

גם בתרגיל זה נבחן את השפעת כל אחד מן המטענים  לחוד, על המטען AQ. מאחר שבתרגיל זה נקבל כוחות הפועלים בזוויות שונות (שלא כמו בתרגילים קודמים), יהיה עלינו  לחבר וקטורית את התוצאות.

בתרגילים האלה, יש לבנות מערכת צירים הניצבים זה לזה. את ראשית הצירים נקבע על אותו מטען,שעליו אנו מחשבים את הכוח השקול.  במקרה שלנו ראשית מערכת הצירים תהיה בדיוק במקום הימצאותו של המטען AQ.

נבחן כיצד משפיע כל מטען לחוד, על AQ:

המטען CQ מפעיל כוח משיכה על המטען AQ, ואילו המטען BQ מפעיל כוח דחייה על המטען AQ.

באיור 7.7 אפשר לראות את ראשית הצירים על המטען הנקודתי AQ ואת אותם כוחות הפועלים על מטען זה כתוצאה מהימצאות המטענים CQ ו-BQ.

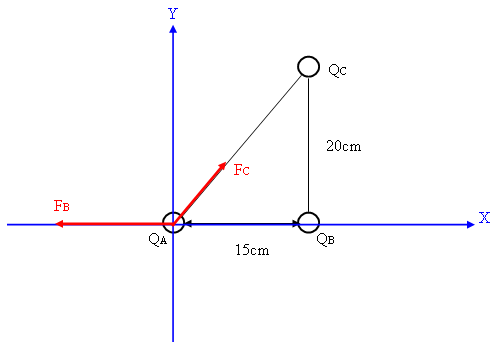
איור 7.7

נחשב תחילה את גודל כל אחד מהכוחות FB ו- FC. לצורך כך ניעזר בחוק קולון:

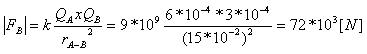
  r_{A – B} זהו המרחק ממטען A למטעןB 

כדי לחשב את גודל הכוח המופעל כתוצאה מן המטען CQ, נמצא את המרחק בין שני המטענים A ו- C, באמצעות משפט פיתגורס:

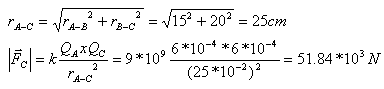
את חישוב הכוח השקול על המטען AQ נעשה על ידי פירוק להיטלים. כלומר נחבר את רכיבי ה- X של הכוחות, נחבר את רכיבי ה- Y של הכוחות ולבסוף נמצא את וקטור הכוח השקול הפועל על המטען AQ (איור 7.8):

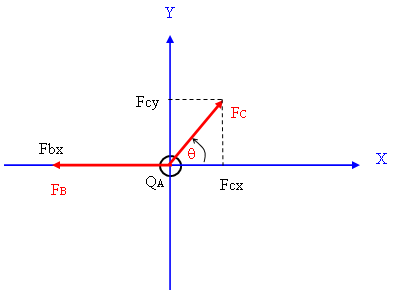
איור 7.8

מאיור 7.8  אפשר לראות כי היטל הוקטור BF על ציר ה- Y שווה לאפס, ואילו היטלו על ציר ה- X שווה לגודל הווקטור (ערך מוחלט) של BF:

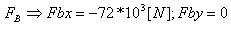
פירוק ההיטלים של הווקטור CF יהיה לפי כללי הטריגונומטריה במשולש ישר זווית:

r_B-C זהו המרחק ממטען B למטען C

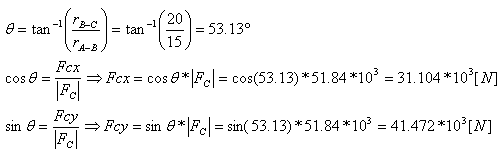
כעת יש לבצע חיבור אלגברי בין ההיטלים:

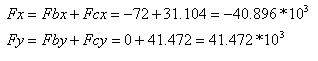
נחשב את גודל הכח AF:

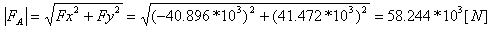
תשובה זו אינה מלאה כיוון שבתרגיל נדרשנו למצוא גם את מגמת הכוח. כדי למצוא את וקטור הכוח הפועל על המטען AQ, יש לחשב את הזווית של AF ביחס לראשית הצירים. לשם כך ניעזר בהיטלים השקולים Fx ו-  Fy (איור 7.9).

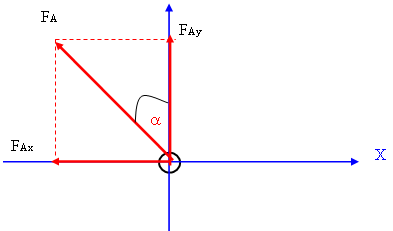
איור 7.9

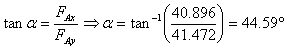
לכן וקטור הכח הפועל על המטען AQ ביחס לראשית הצירים הנו: 90°+44.59°

•   הקודם                                                                                                                             
• המשך