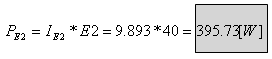תרגיל
דוגמה 11
נתונה הרשת שבאיור 6.50 :
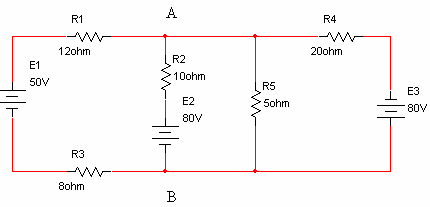
איור 6.50
חשבו את:
א. הפרש
המתחים בין הנקודות A ו- B
ב. זרם
דרך R2 וכיוונו
ג. הספק
הנמסר/נצרך על ידי מקור המתח E3
פתרון
תרגיל דוגמה 11
ראשית עלינו לבדוק אם אפשר לאחד צמתים. בסך הכול
אפשר להציג מעגל הכולל רק שני צמתים, נקבע אחד מהם כצומת הייחוס של המעגל ואת שאר
הצמתים נמספר בסדר רץ, כפי שמוצג באיור 6.51:
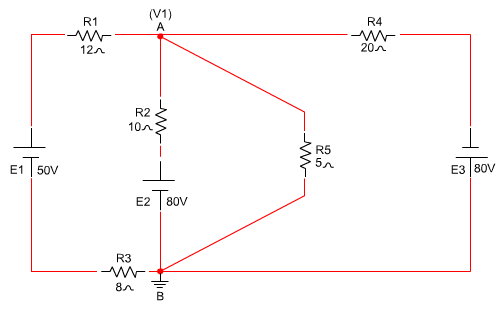
איור 6.51
כלומר עלינו לבנות מטריצה בגודל אחד על אחד
(נעלם אחד). נסמן את הצומת שאין אנו יודעים בו את המתח ביחס לצומת הייחוס בשם V1.
התבנית שאנו צריכים
לבנות נראית כך:
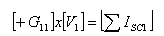
נשתק את מקורות האנרגיה
ונרשום את סכום המוליכויות שמתחברות בין צומת כלשהו לבין הצומת V1 (G11):
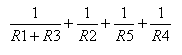
בשלב השני נקצר בין הצמתים A
ו- B ונבדוק מהו הזרם שנכנס או יוצא מצומת V1 (חוט הקצר אמנם משותף לכל הענפים אך הוא
יוצר מסלול קצר לכל ענף בנפרד):
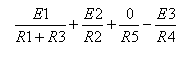
נרשום
משוואה בעבור הצומת V1:
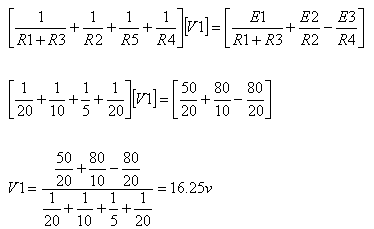
היות שאנו יודעים את כל
ערכי המתחים בצמתים השונים במעגל ביחס לצומת הייחוס, אפשר לענות על סעיפי
השאלה.
א. בכל התרגילים שהצגנו עד כה, חישוב מתח בין שתי נקודות התבסס על
איסוף מתחים בין אותן שתי נקודות. בשיטת מתחי צמתים מאחר ואנו כבר יודעים את המתח
בצמתים השונים, מומלץ לחשב סעיף זה בהסתמך על ההגדרה של UAB,
שפירושה הפרש (פעולת חיסור) המתחים בין צומת A לצומת B.
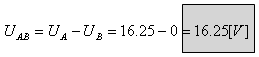
ב. כדי לחשב את הזרם דרך
הנגד R2
נניח כיוון בענף שבו הוא מחובר, ונפעל כפי שתואר בשלושת הדוגמאות הבסיסיות בתחילת
תת הפרק "שיטת מתחי צמתים".
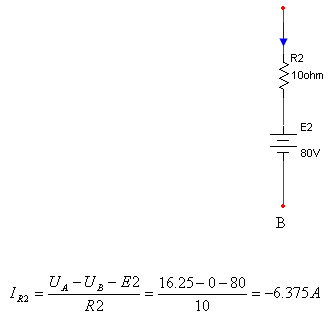
כלומר הזרם בענף דרך הנגד R2 הפוך
מההנחה שקבענו
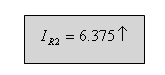
הערה:
אפשר לקבוע גם את כיוון
הזרם בוודאות (ללא צורך בהנחה) אם יודעים את המתח בצמתים השונים ואת גודל מקורות
המתח בענף.
ג. תחילה נחשב את הזרם דרך E3 (נניח שהזרם זורם מ- A ל- B):
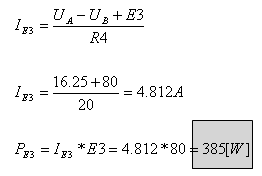
מקור המתח E3 מספק אנרגיה (אפשר לראות זאת
על פי כיוון הזרם שהתקבל בענף).
תרגיל דוגמה 12
למד הזרם, במעגל שבאיור 6.52, התנגדות פנימית של Ω4
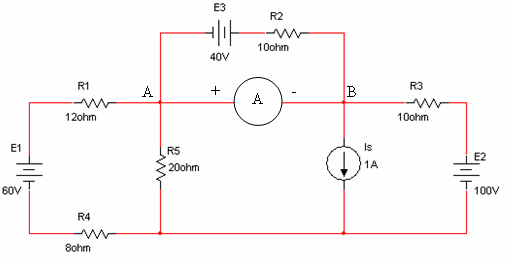
איור 6.52
חשבו את:
א. הפרש
המתחים בין הנקודות A ו- B
ב. מה
תהיה קריאת מד הזרם
ג. הספק
הנמסר/נצרך על ידי מקור הזרם (ציין את סוגו)
פתרון תרגיל דוגמה 12
נאחד את שני הצמתים התחתונים לאחד. בסך הכללי
אפשר להציג מעגל הכולל שלושה צמתים, נקבע אחד מהם כצומת הייחוס של המעגל. נצייר
מעגל חדש כאשר במקום מד הזרם נסרטט נגד חשמלי בעל ערך של 4Ω כמתואר באיור 6.53.
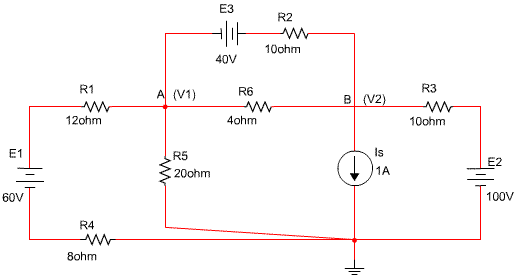
איור 6.53
נבנה את מערכת המשוואות באופן מטריציאלי תוך
שימוש בתבנית של 2 משוואות (כמספר הצמתים פחות צומת הייחוס):
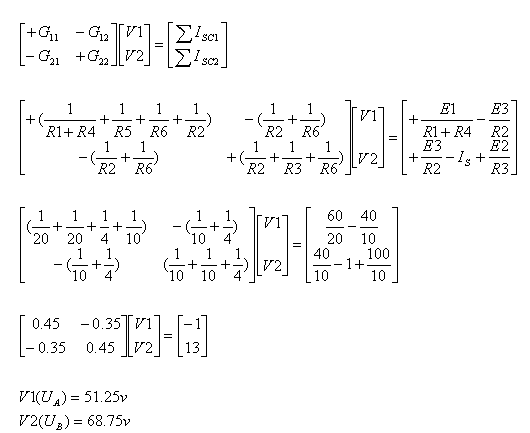
כעת אפשר לענות על סעיפי השאלה:
א.
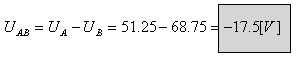
ב. נחשב
את הזרם דרך הנגד R6 (שמבטא את התנגדות מד הזרם):
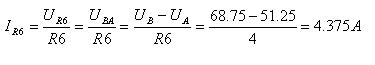

ג. הספק על מקור זרם יחושב על ידי מכפלת זרם המקור במתח השורר על
הדקיו.
אפשר לראות שהמתח עליו שווה למתח בין הנקודות B
ובין האדמה.
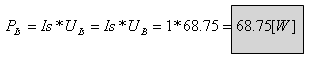
על פי קוטביות המתח בין הדקי מקור הזרם אפשר לקבוע האם הוא
מספק אנרגיה או צורך. מאחר שחץ המתח על מקור
הזרם הפוך ללחץ זרם המקור, מכאן נובע שמקור הזרם צורך אנרגיה.
תרגיל דוגמה 13
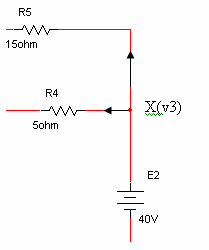
במעגל שבאיור 6.54 מחובר מקור מתח אידאלי בעל כא"מ של 40v,
בין הצמתים X ל- Y.
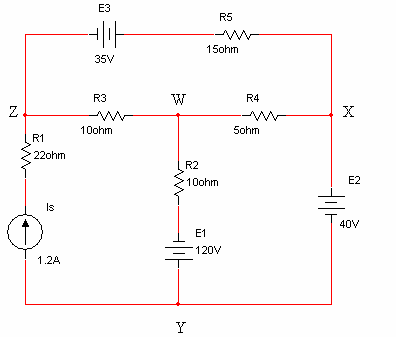
איור 6.54
חשבו את:
א. הזרם דרך הנגד R ;
ב. ZWU;
ג. ההספק הנמסר על ידי
מקור המתח E2.
פתרון תרגיל דוגמה 13
אי אפשר לאחד צמתים במעגל, לכן נתחיל
בקביעת צומת ייחוס למעגל (Y) - ראו איור 6.55
הערה:
במעגלים שיש בהם מקורות מתח אידאלים, מומלץ לקבוע את צומת הייחוס באחת הרגליים של
מקור המתח האידאלי.
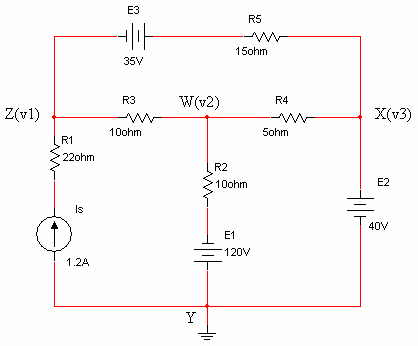
איור
6.55
בעבור צומת X אנו יודעים מהו הפוטנציאל ביחס לנקודת
הייחוס, כי בין צומת X לאדמה קיים מקור מתח אידאלי. על אף שרק בשני צמתים אין אנו יודעים
את המתח, אנו נבנה תחילה תבנית של 3 משוואות (כמספר צומתי המעגל פחות צומת
הייחוס), ובהמשך הפתרון נצטמצם לשתי משוואות.
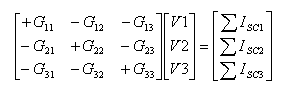
תזכורת:
(+) מציין את סכום כל המוליכיות שיוצאות מאותו
הצומת כאשר מקורות האנרגיה משותקים!
(-) מציין את סכום המוליכויות שמתחברות בין שני
צמתים הרשומים בתבנית כאשר מקורות האנרגיה משותקים!
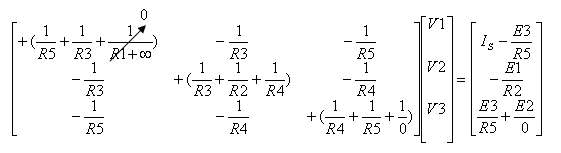
מהתבנית הרשומה התקבלה שורה (שלישית) שבה מצוי
הערך ¥
(חלוקה באפס נותנת אינסוף). בכל פעם כשיהיה מחובר מקור מתח אידאלי במעגל, צריך
להופיע הסימן ¥.
בתבנית יש למחוק את השורה בה הופיע הערך אינסוף
(ללא הערך של V3 בוקטור המתחים) !!!
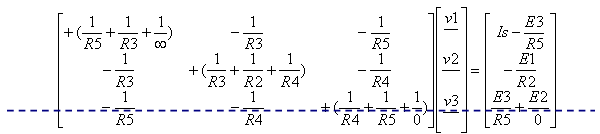
עלינו לסדר מחדש את
ההצגה המטריציאלית כך שיופיעו רק 2 משוואות עם שני נעלמים. לשם הבנת התהליך, נרשום
רק את 2 המשוואות שלא מופיע בהם הערך אינסוף בצורה המתמטית הרגילה:
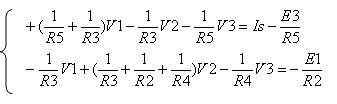
את ערכו של V3
אנו יודעים – פוטנציאל המתח בנקודה X . לכן כשנציב את ערכו המספר (40V), נקבל 2 משוואות עם שני נעלמים.
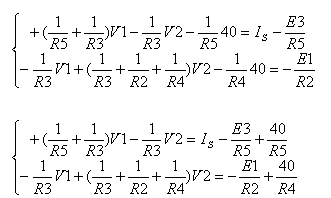
נציג שוב זאת בצורה
מטריציאלית:
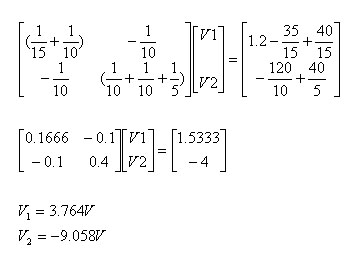
יש להתאים את הערך
המספרי לכל פוטנציאל של מתח:
א. נניח שכיוון הזרם בענף הוא מ- Y
ל- W:
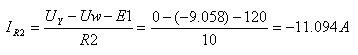

ב.
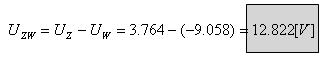
ג. כדי לחשב את הזרם דרך מקור המתח E2
נחשב תחילה את הזרם דרך הנגדים R4 ו- R5.
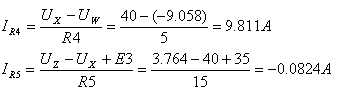
הערה לחישוב הזרמים
בענפי המעגל וקביעת כיוונים:
בחישוב הזרם דרך הנגד R4
הצבנו XU פחות YU, כלומר אם התוצאה חיובית, אכן הזרם כיוונו
מ- X
ל- Y,
שאם לא כן הכיוון הפוך.
בנוגע לזרם דרך הנגד R5
הצבנו ZU פחות XU, כלומר הנחנו שהזרם כיוונו מנקודה Z
לנקודה Y.
באותו ענף (בהסתמך על הכיוון שהנחנו) מופיע מקור מתח E3 שעוזר לזרם שהנחנו, לכן הוספנו אותו להפרש
מתחים במונה, אך אם הוא היה מתנגד לכיוון הזרם שבחרנו, היינו מבצעים פעולת
חיסור.
מאחר שתוצאת הזרם
שלילית בנגד R5, הרי שהזרם דרכו בענף הוא מנקודה X ל- Z.
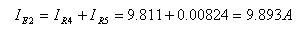
לכן את הזרם דרך מקור
המתח E2 נחשב
באמצעות חוק הזרמים של קירכהוף.
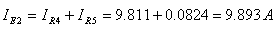
לכן מקור המתח E2 מספק
אנרגיה והספקו: