קורס בתורת החשמל מאת יוסי יאשי

(Matrix equation notation)

אפשר לחשב את הפוטנציאל בצומתי המעגל ביחס לצומת הייחוס גם בעזרת רישום מקוצר של המשוואות. לפניכם תבנית לשלושה מתחי צמתים (שלוש משוואות) המתאימים לפתרון מעגל עם ארבעה צמתים (אחד מהם הוא צומת הייחוס):

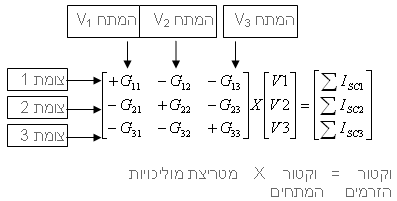
כאשר:

א. המספרים שמופיעים בקטן בצד האות G במטריצת המוליכויות מתארים את מיקומו של האיבר במטריצה. למשל, 32 פירושו שורה 3 עמודה שנייה (הספרה הראשונה מציינת שורה והשנייה את העמודה).

ב. האלכסון במטריצת המוליכויות חיובי תמיד. גודל המטריצה תלוי במספר צומתי המעגל (פחות אחד).  אם היה צומת נוסף במעגל, האלכסון היה גדל באחד וכך הלאה.

ג.  האות G שבצדה (+) מציינת  את סכום כל המוליכויות שמתחברות לצומת הנבדק כאשר כל מקורות האנרגיה משותקים . למשל,  G₂₂ משמעו סכום המוליכויות שמתחברות לצומת 2. ה (+) מציין שזהו מספר חיובי.

ד.  האות G שבצדה (-)  מציינת את סכום המוליכויות המשותפות המחוברות בין שני צמתים כאשר כל מקורות האנרגיה משותקים.. למשל, G₁₃ משמעו סכום המוליכויות שמחוברות בין צומת 1 לצומת 3. הסימן  (-) מציין שזהו מספר שלילי.

ה. 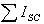 מציין את הסכום  של זרמי הקצר של כל הענפים שמחוברים לצומת הנבדק. למשל 

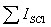
מתייחס לסכום כל זרמי הקצר של הענפים המחוברים לצומת 1. אם יש מקורות מתח בענף, גודלו של זרם הקצר בענף יהיה חלוקה של מקור המתח בנגדי הענף וקוטביות זרם הקצר תיקבע לפי קוטביות מקור האנרגיה – מקור מתח עם + לכיוון הצומת הנבדק יגרום לזרם קצר חיובי, מקור מתח עם – לכיוון הצומת הנבדק יגרום לזרם קצר שלילי, מקור זרם הנכנס לצומת יסומן בקוטביות חיובית, ואילו מקור היוצא מן הצומת יסומן בקוטביות שלילית. בענף ללא מקור אנרגיה יתקבל זרם קצר השווה לאפס.

ו. בפתרון רשתות בשיטה הזאת אין צורך בהמרה של מקורות זרם.

•   הקודם                                                                                                                             
• המשך