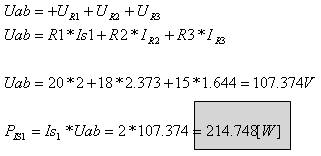קורס בתורת החשמל מאת יוסי יאשי

תרגיל דוגמה 6

נתונה הרשת שבאיור 6.25:

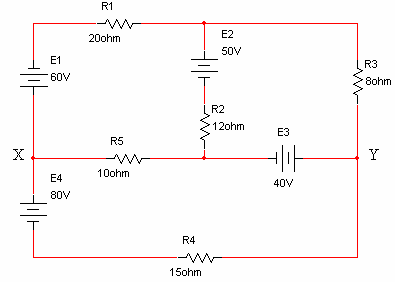
איור 6.25

חשבו את:

א.      זרם דרך הנגד R4 וכיוונו

ב.       הספק המתפתח בנגד R2

ג.        הפרש המתחים בין הנקודות X ו- Y

פתרון תרגיל דוגמה 6

נקבע את כל זרמי החוג עם כיוון השעון ונבנה שלוש משוואות בצורה מקוצרת:

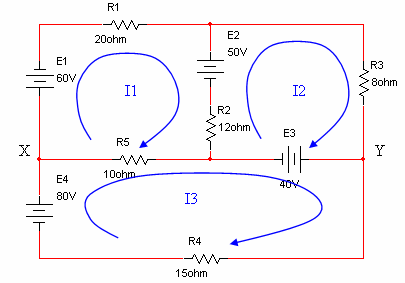
איור 6.26

אפשר לחשב את  זרמי החוגים על ידי פתרון שלוש משוואות עם שלושה נעלמים. זוהי דרך ארוכה במקצת.

נציג כאן דרך אחרת הנקראת בשם שיטת קרמר לפתרון מערכת משוואות. גם היא דרך ארוכה אך ניתנת לחישוב מהיר באמצעות מחשבון כיס.

ראשית, נרשום את משוואת החוגים המטריציאלית, המתאימה למעגל שבדוגמה:

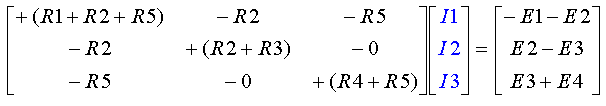
נציב ערכים ונקבל:

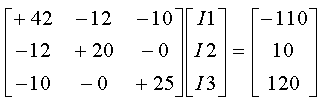
נגדיר כעת את המושג דטרמיננט:

הדטרמיננט של מטריצה,מסומן ב- Δ. זהו המספר המתקבל כתוצאה מן החישוב הזה:

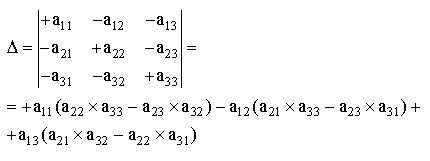
הערה: דטרמיננט של מטריצה 2 על 2 יחושב כך:

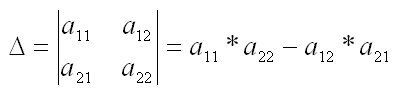
נציב את המספרים ממטריצת ההתנגדויות שלמעלה ונפתור עוד שלושה דטרמיננטים, ונסמן אותם ב-

 :Δ₁,  Δ₂, Δ₃

 Δ₁הוא הדטרמיננטה של המטריצה המתקבלת כאשר מחליפים את עמודה 1 של מטריצת ההתנגדויות ווקטור המתחים. באופן דומה מתקבל Δ₂ כשמחליפים את עמודה 2 בווקטור המתחים ו- Δ₃ כשמחליפים את עמודה 3 בווקטור המתחים:

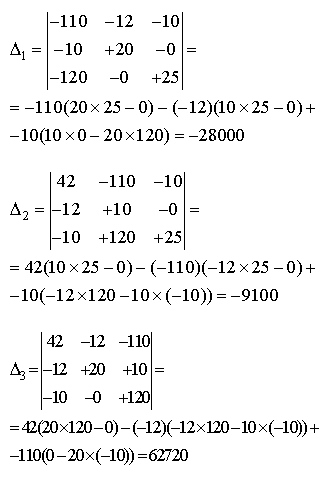
כעת אפשר לפתור באמצעות דטרמיננטות ולמצוא את ערכם של המקדמים I1, I2, I3. 

באופן הזה:

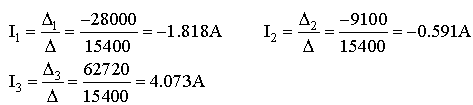
אפשר גם להיעזר במחשבון לצורך מציאת הזרמים:

I1= -1.818[A]  ;  I2= -0.59[A]   ;   I3= 4.072[A]

שני הזרמים שהתקבלו עם סימן שלילי, בפועל זורמים הפוך מכפי שקבענו בתחילת התרגיל, כלומר נגד כיוון השעון. נסמן על גבי המעגל את כיוונם האמיתי ונרשום אותם עם סימן חיובי.

איור 6.27

 וכאן אפשר לומר שסיימנו ללמוד את שיטת זרמי החוגים. כעת, לאחר השגת המטרה - מציאת זרמי החוגים הבלתי תלויים, אפשר להשיב על סעיפי התרגיל:

א.    זרם החוג I3 עובר דרך הנגד R4, לכן:

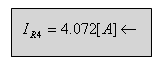
ב.   כדי לחשב את ההספק בנגד R2, נמצא תחילה את הזרם האמיתי דרכו. דרך הנגד R2 עוברים שני זרמי חוג – I1 וגם I2. בפועל דרך הנגד R2 עובר זרם אמיתי אחד. את הזרם הזה אפשר לחשב באמצעות כלל ההרכבה על שני זרמי החוג שעוברים דרכו. מאחר שזרם החוג I1 עובר דרכו בכיוון מעלה ואילו זרם החוג I2 עובר דרכו בכיוון מטה, הרי שהזרם האמיתי יהיה תוצאה של חיסור זרמי החוג (כי הם בכיוונים שונים זה לזה) וכיוונו יהיה ככיוון הזרם הגדול:

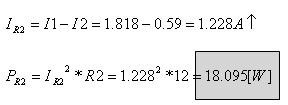
ג. למציאת הפרש המתחים בין שתי הנקודות, נבחר במסלול הקצר ביותר לאיסוף המתחים מנקודה X לנקודה Y. מומלץ, כפותרים בשיטת זרמי חוגים לבחור במסלולים שבהם אין הרכבה של זרמים. לכן נבחר בענף התחתון של המעגל ונסמן בו את קוטביות המתחים:

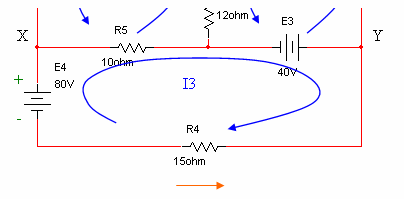
איור 6.28 

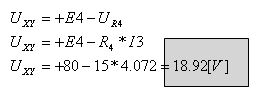
תרגיל דוגמה 7

נתונה הרשת שבאיור 6.29:

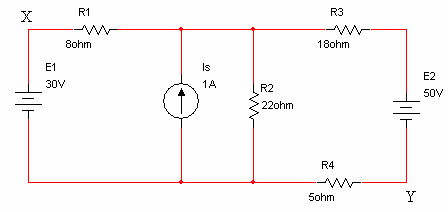
איור 6.29

חשבו את:

א.      הספק המתפתח בנגדR4

ב.       Uxy

ג.       זרם דרך הנגד R2 וכיוונו

ד.      הספק הנמסר/נצרך על ידי מקור הזרם. ציינו האם המקור צורך או מספק אנרגיה.

פתרון תרגיל דוגמה 7

מעגלים שבהם מחוברים מקורות זרם אי אפשר לפתור באופן רגיל בשיטת זרמי החוגים, בצורה המקוצרת. פתרון בשיטה מקוצרת זו, מחייב אותנו להחליף את מקור האנרגיה – מקור זרם, במקור אנרגיה אחר – מקור מתח, אשר מספק/צורך את אותה אנרגיה במעגל.

כדי להמיר ממקור זרם למקור מתח, יש לפעול על פי הכלל הזה (המרה זו תוכח בהמשך הפרק):

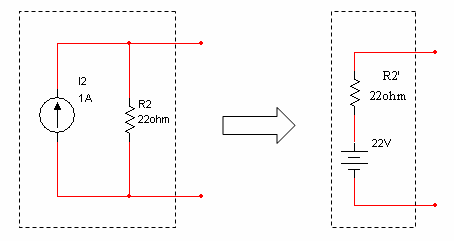
איור 6.30

יש לאתר את הנגד שמחובר במקביל עם מקור הזרם ולכפול אותו בגודל מקור הזרם. תוצאה זו שתתקבל, תהווה את גודלו של מתח המקור החלופי, כשהתנגדות הנגד שתהיה מחוברת בטור למקור מתח זה, תהיה בעלת ערך זהה לנגד שחובר במקביל למקור הזרם. את קוטביות מקור המתח החלופי קובע כיוון מקור הזרם: ראש החץ של מקור הזרם מסמן את הקוטביות החיובית במקור המתח. 

כא"מ מקור המתח וההתנגדות הפנימית שבטור אליו מהווים יחד מקור שקול למקור הזרם. בפועל, הרכיבים האלה אינם קיימים במעגל, לכן נסמנם באופן הזה (הסימן ' מציין רכיב וירטואלי שלא באמת קיים במעגל המקורי):

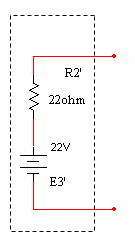
איור 6.31

כעת נסרטט את המעגל שבאיור 6.31 לאחר ביצוע ההמרה (נוציא מן המעגל המקורי את מקור הזרם והתנגדותו שבמקביל, ובמקומם נחבר מקור מתח ונגד בטור):

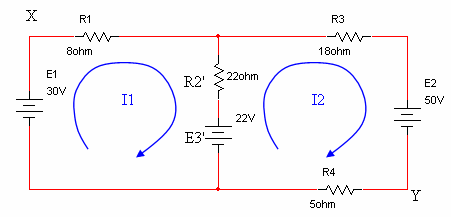
איור 6.32

נסמן את זרמי החוג עם כיוון השעון ונפעל על פי השיטה המקוצרת:

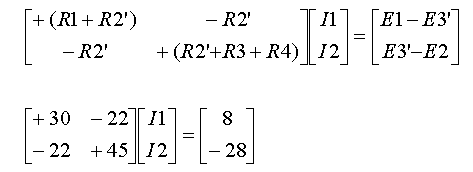
ניעזר במחשבון לקבלת ערכי הזרמים I1 ו- I2:

I1= -0.295A   ;   I2= -0.766A

נשרטט שוב את המעגל כולל כיווני זרמי החוג האמיתיים:

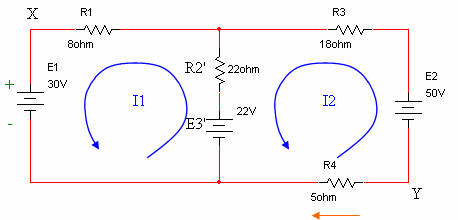
איור 6.33 

א.   חישוב ההספק בנגד R4

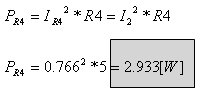
ב.   נבחר מסלול מנקודה X לנקודה Y (דרך מקור המתח E1 והנגד R4):

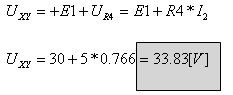
ג.   במעגל שעליו אנו עובדים לא קיים הנגד R2, אלא במקומו מופיע הנגד  R2’. משמעות הדבר שאי אפשר לחשב את הזרם דרך הנגד R2 במעגל זה. במקרים מסוג זה, חובה לחזור למעגל המקורי, המכיל את הנגד R2 המקורי.

חשוב לזכור ששאר הנגדים שמופיעים במעגל שלאחר ההמרה, הם אותם נגדים שמחוברים גם במעגל המקורי. כלומר דרך הנגד R1 עובר זרם החוג I1 , ואילו דרך הנגדים R3 ו- R4 עובר זרם החוג I2.

לכן, כל מה שעלינו לעשות כדי למצוא את הזרם דרך הנגד R2 הוא להשתמש בחוק הזרמים של קירכהוף. תחילה נחשב את הזרם Ix ורק לאחר מכן את הזרם דרך הנגד R2.

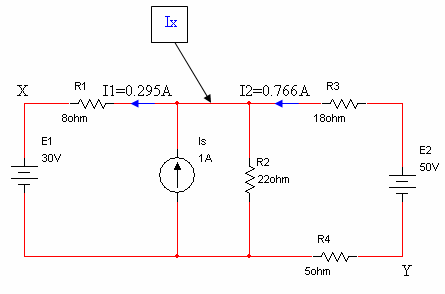
איור 6.34

את הזרם Ix הזורם בכיוון ימין בענף העליון המסומן במעגל, נחשב כך:

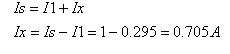
כעת אפשר לחשב גם את הזרם דרך הנגד R2:

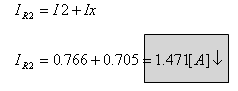
ד.   כדי לחשב את הספק מקור הזרם יש לכפול את המתח על הדקיו בזרם המקור. המתח על הדקי מקור הזרם שווה למתח על פני הנגד R2 ולכן:

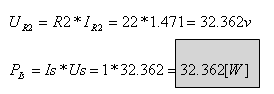
מקור הזרם מספק אנרגיה למעגל כי קוטביות המתח עליו חיובית (על ראש החץ של מקור הזרם מופיע פוטנציאל חיובי).

תרגיל דוגמה 8

נתונה הרשת שלפניכם שבאיור 6.35:

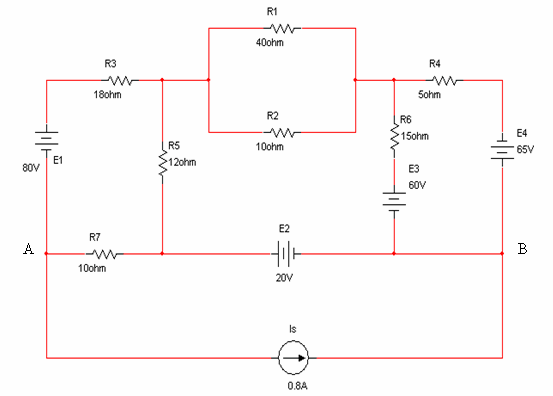
איור 6.35

חשבו את:

א.    ההספק בנגד R5;

ב.    הזרם דרך הנגד R2  וכיוונו;

ג.      הפרש המתחים בין הנקודות A ו- B;

ד.     הספק מקור המתח  E2 (ציינו את אופן פעולתו צורך/מספק).

פתרון תרגיל דוגמה 8

כדי לפתור רשת זו בשיטת זרמי חוגים באופן המקוצר, עלינו לבצע המרה של מקור הזרם במעגל. ההמרה במעגל זה איננה סטנדרטית כיוון שמקור הזרם מחובר במקביל לענף המכיל כמה רכיבים. במקרה מסוג זה, יש לראות את מקור הזרם כהתקן שמחובר במקביל לכל אחד מן הרכיבים בנפרד. ההוכחה של  הטענה הזאת אינה נכללת במסגרת הקורס.

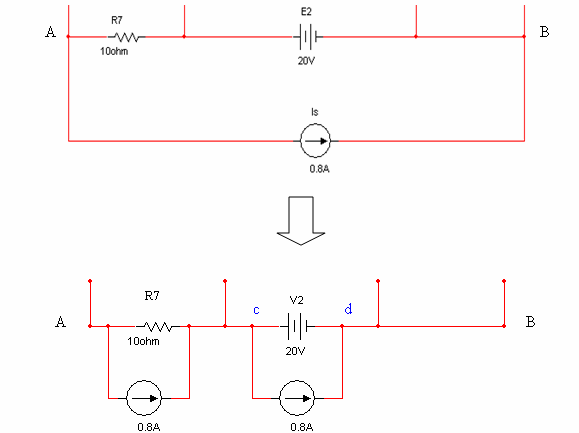
איור 6.36 

כתוצאה מכך התקבלו שני סוגי חיבורים של מקור זרם: האחד, המרה סטנדרטית של מקור זרם במקביל עם נגד. לעומתו, ישנו מקור זרם במקביל למקור המתח. לצורך הבנת המרה זו, ננסה לענות על שלוש שאלות מנחות:

אם כך אפשר לומר שלמקור הזרם אין השפעה על המתח בין הדקי מקור המתח. מאחר שבשיטת זרמי החוגים, המשוואות שמיוצרות הן תוצאה של חוק המתחים של קירכהוף, הרי שלמקור הזרם בשלב זה של רישום המשוואות אין שום משמעות ואפשר להורידו.

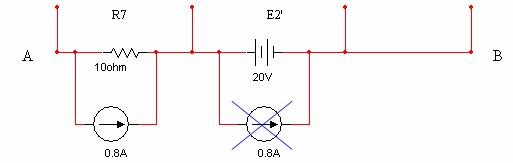
איור 6.37 

לכן הענף שיתקבל לאחר המרת מקור הזרם Is ייראה כך:

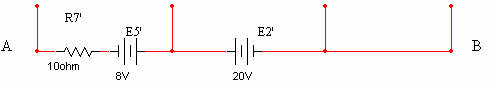
נסרטט את המעגל המקורי לאחר ביצוע ההמרה של מקור הזרם:

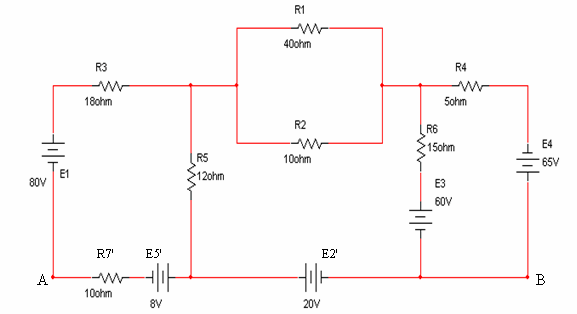
איור 6.38

הערה: כל אותם נגדים/מקורות מתח שמסומנים עם ' , הם לא אותם רכיבים מהמעגל המקורי שלפני ביצוע ההמרה.

אפשר ליצור ללא שום בעיה ארבע משוואות לפתרון המעגל, אך בראייה קדימה, נצטרך להתמודד עם פתרון של ארבע משוואות עם ארבעה נעלמים. לצורך כך, תמיד מומלץ לבדוק, לפני כתיבת המשוואות, האם אפשר לצמצם את כמות החוגים הבלתי תלויים במעגל. צמצום מסוג זה יקטין את כמות המשוואות ובכך יקל על פתרון התרגיל. צמצום רכיבים במעגל מומלץ רק אם ביכולתו לצמצם את מספר החוגים הבלתי תלויים.

נחליף את הנגדים R1 ו- R2  בנגד אחד שקול ובכך נצמצם חוג.

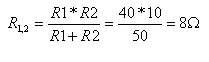
נסרטט את המעגל לאחר צמצום החוג ונתחיל בפתרון באמצעות שיטת זרמי חוגים.

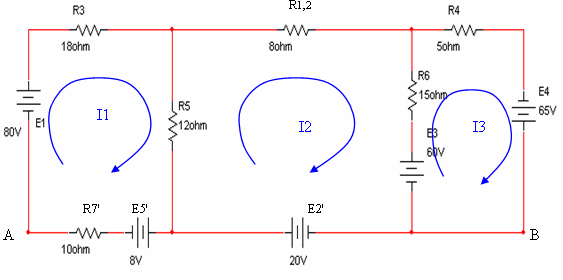
איור 6.39  

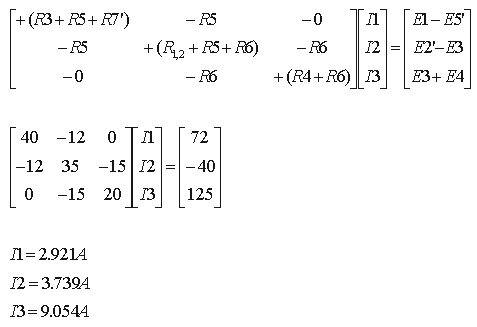
א.   נחשב תחילה את הזרם שעובר דרך הנגד R5. דרך נגד זה עוברים שני זרמי חוג (I1 וגם I2), לכן נבצע הרכבה בין הזרמים. מאחר שדרך הנגד הזרמים הם בכיוונים הפוכים (I1 יורד דרכו ואילו I2 עולה), נחסר גדול פחות קטן:

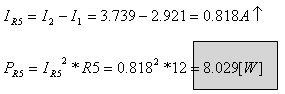
ב.   הנגד R2 אינו מופיע במעגל שבעבורו חישבנו את זרמי החוג, אך אפשר לראות שזרם החוג I2 מתפצל לשני נגדים R1 ו- R2 שמחוברים במקביל. לכן על פי כלל מחלק הזרם אפשר למצוא את הזרם דרך הנגד R2 וכיוונו.

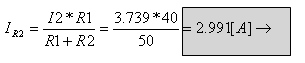
ג.   נסמן מסלול לאיסוף המתחים בין הנקודות A ל- B:

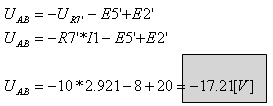
הערה:

הפרש הפוטנציאלים בין הנקודות AB הוא שלילי. משמעות הדבר היא שהפוטנציאל בנקודה B גבוה מן הפוטנציאל בנקודה A. אם יחובר צרכן בין הנקודות האלה, כיוון הזרם דרך הצרכן יהיה מן הפוטנציאל הגבוה לנמוך, כלומר מנקודה B לנקודה A.

ד. את הסעיף הזה אי אפשר לפתור במעגל זה, מכיוון שלא קיים מקור מתח E2 (המקור שמחובר במעגל הנו E2'). לכן נחזור למעגל המקורי עם התוצאות של הזרם ממעגל זה ובעזרת שימוש בחוק הזרמים של קירכהוף, נמצא את הזרם דרך מקור המתח E2.

למשל, את תוצאות הזרם דרך הנגד R5 ומקור המתח E1 במעגל הזה, אפשר להעביר גם למעגל המקורי משום שרכיבים אלו לא נפגעו כתוצאה מההמרה של מקור הזרם.

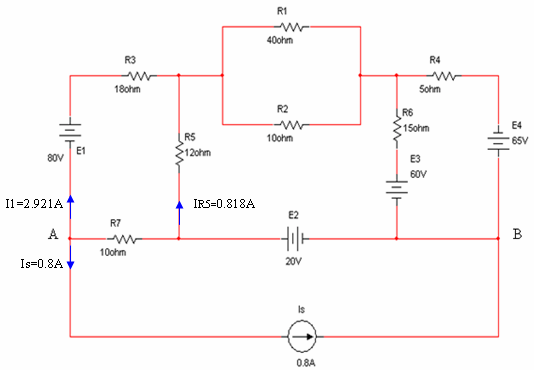
איור 6.40

על פי חוק הזרמים של קירכהוף הזרם דרך R7 נכנס לצומת A (כי שני הזרמים האחרים יוצאים ממנו).

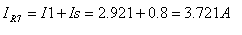
באותו אופן נחשב את הזרם דרך מקור המתח E2:

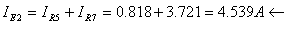
כעת אפשר לחשב את ההספק שנמסר על ידי מקור המתח E2:

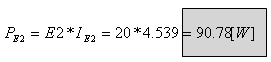
תרגיל דוגמה 9

נתונה הרשת שבאיור 6.41

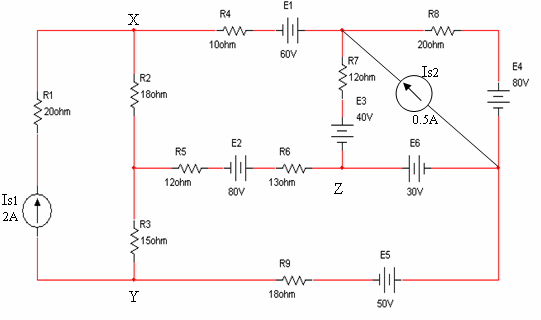
איור 6.41 

חשבו את:

א.      ההספק של מקור המתח E5     

ב.      זרם דרך הנגד  R7 וכיוונו

ג.        הפרש הפוטנציאלים XZU          

ד.       הספק מקור הזרם Is1         

פתרון תרגיל דוגמה 9

כדי לפתור רשת זו בשיטת זרמי חוגים באופן המקוצר יהיה עלינו להמיר תחילה את מקורות הזרם.

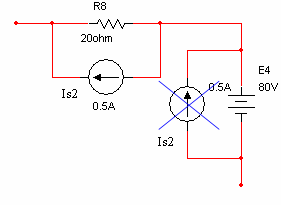
המרת מקור הזרם Is2 – נבצע המרה על הענף החיצוני שמחובר במקביל אליו, הכולל את מקור המתח E4 והנגד R8 (יש לשים לב לכיוון מקור הזרם בעת ביצוע ההמרה).

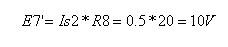
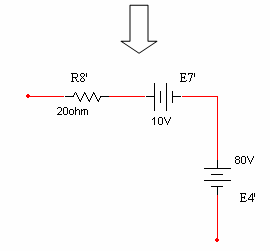
המרת מקור הזרם Is1 –  מקור הזרם אינו מחובר במקביל לשום ענף!!! הנגד R1 מחובר בטור אליו ולכן נראה שאי אפשר לבצע המרה (ראו איור 6.41) .

לפי התשובות שהתקבלו אפשר לראות שהזרם בענף שבו מצוי הנגד R1 קבוע, ולנגד R1 אין השפעה על עצמת הזרם בענף. מכאן אפשר להסיק שכל אותם רכיבים שמחוברים בטור למקור הזרם אינם משפיעים על זרמי המעגל, ולכן אפשר להתעלם מהם בעת חישובי הזרמים.

ערכו של הנגד R1 הוא זה שיקבע את הספקו של מקור הזרם Is1. שינוי בערכו ישנה את מפל המתח על מקור הזרם ובכך את הספקו.

לשם ביצוע ההמרה נתעלם מהנגד R1:

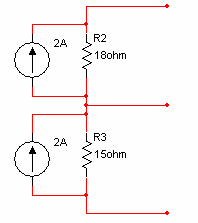
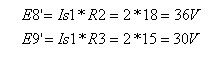
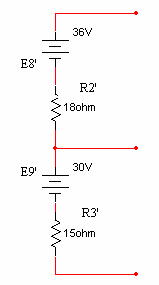
נסרטט את המעגל לאחר המרות מקורות הזרם, נסמן זרמי חוג ונפתור.

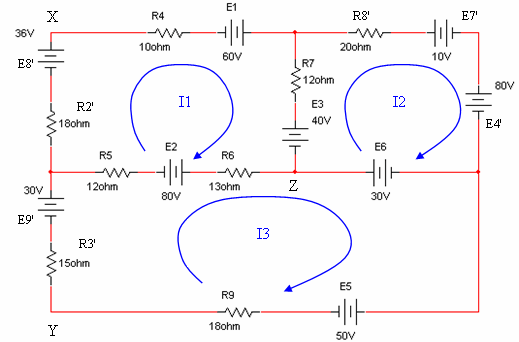
איור 6.42

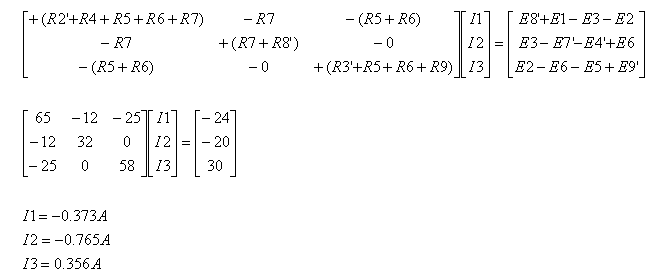
זרמי החוג I1 ו- I2 בפועל זורמים נגד כיוון השעון.

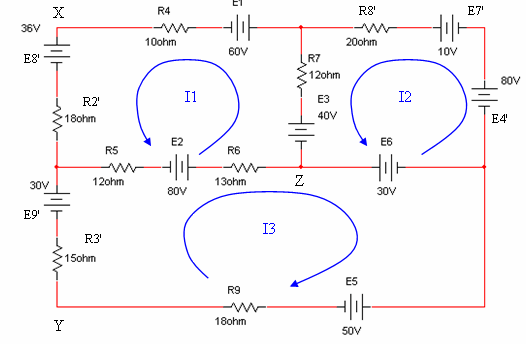
איור 6.43

א.  

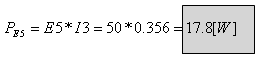
ב.   הנגד R7 חש בשני זרמי החוג I1 ו- I2 (זרם החוג I1 עולה דרך הנגד ואילו זרם החוג I2 יורד דרכו). נבצע הרכבה בין זרמי החוג למציאת הזרם האמיתי דרך הנגד R7:

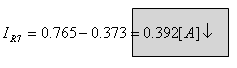
ג.   נבחר מסלול מנקודה X לנקודה Z:

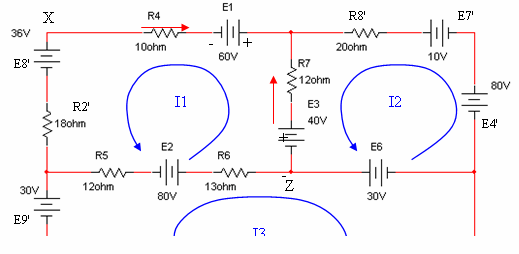
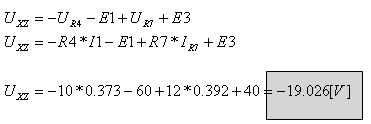
ד.   מקור הזרם Is1 לא מחובר במעגל הנוכחי, לכן עלינו לחזור למעגל המקורי כדי לחשב את הספקו של מקור זרם זה. נזכיר, שלשם מציאת הספק מקור זרם יש לכפול את זרם המקור במפל המתח עליו.

לשם מציאת מפל המתח על מקור הזרם Is1, נגדיר שתי נקודות a ו- b המציינות את הדקי מקור הזרם. חישוב המתח בין הנקודות ab יאפשר לנו לקבוע את הספקו של מקור הזרם Is1.

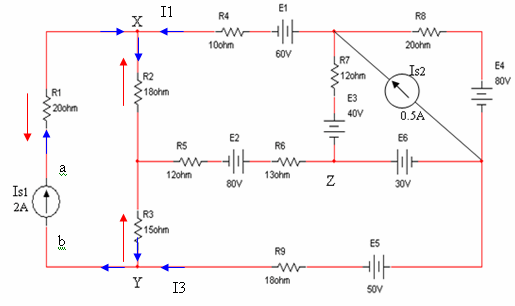
איור 6.44

נחשב תחילה את הזרם דרך הנגדים R2 ו- R3, כך נוכל לבחור במסלול של הנגדים R1, R2, R3 בחישוב המתח על הדקי מקור הזרם (Uab).

על פי חוק הזרמים של קירכהוף:

חישוב המתח על הדקי מקור הזרם:

•   הקודם                                                                                                                             
• המשך