קורס בתורת החשמל מאת יוסי יאשי

(Matrix equation notation)

רישום משוואות באופן זה מחייב אותנו לקבוע את כל כיווני זרמי החוג באותו כיוון (מומלץ לקבוע את כולם עם כיוון השעון). במצב זה נפעל על פי תבנית קבועה וידועה מראש ליצירת המשוואות המתמטיות.

נציג למשל תבנית לשלושה זרמי חוג (שלוש משוואות) בצורה מטריציאלית :

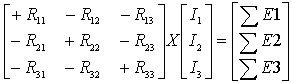
וקטור המתחים = וקטור הזרמים X מטריצת התנגדויות

כאשר:

א.    הספרות שמופיעות בקטן בצד האות R במטריצת ההתנגדויות מתארות את מיקומו של האיבר במטריצה. למשל, 32 פירושו שורה 3 עמודה שנייה (הספרה הראשונה מציינת שורה והשנייה את העמודה).

ב. האלכסון במטריצת ההתנגדויות חיובי תמיד. גודל המטריצה תלוי במספר חוגי המעגל. בעבור חוג אחד נקבל מטריצה של 1 על 1. בעבור שני חוגים נקבל מטריצה של 2 על 2 וכך הלאה.

ג.     האות R שבצדה (+) מציינת  את סכום הנגדים בחוג המתאים. למשל,  R₂₂ משמעו סכום הנגדים בחוג מספר 2. ה (+) מציין שזהו מספר חיובי.

ד.      האות R שבצדה (-)  מציינת את סכום הנגדים המשותפים בין שני חוגים. למשל, R₁₃ משמעו סכום הנגדים המשותפים בין חוג מספר 1 לחוג מספר 3. ה (-) מציין שזהו מספר שלילי.

ה. 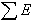      מציין את סכום  המתחים של כל מקורות המתח בחוג שבו אנו מצויים. מקור מתח המספק אנרגיה יסומן בקוטביות חיובית, ואילו מקור צורך אנרגיה יסומן בקוטביות שלילית. בחוג מספר 1, כיוון זרם החוג I1 הוא זה שיקבע אם המקורות בחוג צורכים או מספקים אנרגיה. בחוג מספר 2, כיוון זרם החוג I2 הוא זה שיקבע וכך הלאה.

ו.     אי אפשר לפתור בשיטה זו כשבמעגל מחוברים מקורות זרם. לכן בשלב הראשוני נפתור רשתות ללא מקורות זרם, ובשלב המאוחר יותר ניתן מענה לבעיה זו.

•   הקודם                                                                                                                             
• המשך