קורס בתורת החשמל מאת יוסי יאשי

(Converting star to triangle)

בכל המעגלים שפתרנו עד כה, היה אפשר לפשט את נגדי המעגל על ידי מציאת קבוצת נגדים בחיבור מסוים והחלפתם בנגד שקול. יש מעגלים שבהם מחוברים קבוצת נגדים, אך אי אפשר לומר עליהם אם הם מחוברים בטור או במקביל.

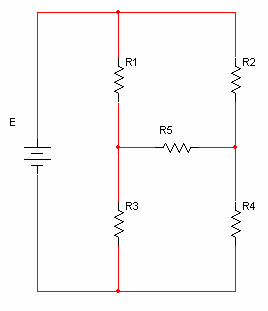
איור 6.1

במעגל הנתון באיור 6.1, אי אפשר לחשב באופן רגיל את ההתנגדות השקולה ש"רואה" מקור המתח. הסיבה לכך, שאין שום נגד במעגל שמחובר בטור או במקביל עם נגד אחר.

טענה 1:

בסוג כזה של מעגלים שבו מחוברים לפחות שלושה נגדים שאי אפשר לומר עליהם שהם בטור או במקביל, "מסתתר" לו לפחות כוכב אחד או משולש אחד.

כוכב מוגדר כשלושה נגדים המחוברים ביניהם עם נקודת צומת אחת מרכזית.

משולש מוגדר כשלושה נגדים המחוברים בין שלושה צמתים.

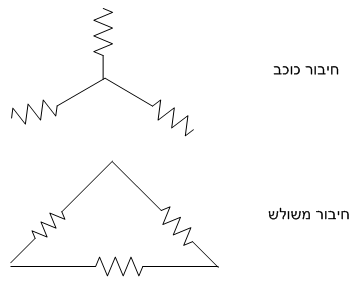
טענה 2:

כל כוכב, אפשר להחליף במשולש, המכיל שלושה נגדים אחרים r₁,_,r₂, r₃, בלי לשנות את צריכת ההספק הכללית במעגל. כמו כן אפשר להחליף כל משולש בכוכב. החלפה זו נקראת בשם המרה והיא דרושה לצורך פישוט המעגל.

הפרש הפוטנציאלים בין הנקודות במעגל לפני ההמרה ואחרי ההמרה נשאר ללא שינוי!

המרה ממשולש לכוכב

במעגל המתואר באיור 6.2  יש שני משולשים (משולש עליון ומשולש תחתון). לצורך פישוט המעגל נמיר משולש אחד בלבד – נבחר במשולש התחתון.

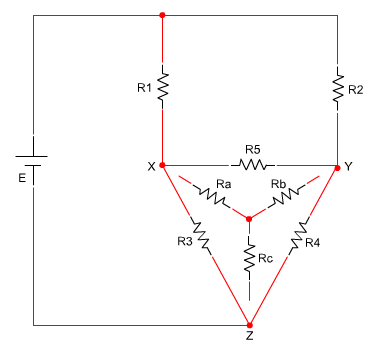
איור 6.2

את נגדי הכוכב החדשים אפשר לחשב כך:

כלומר, הנגד בכוכב מתקבל על ידי מכפלת הנגדים משני צדדיו במשולש, לחלק לסכום נגדי המשולש.

כעת נסרטט את המעגל החדש (איור 6.3) כשנגדי הכוכב יחליפו את נגדי המשולש:

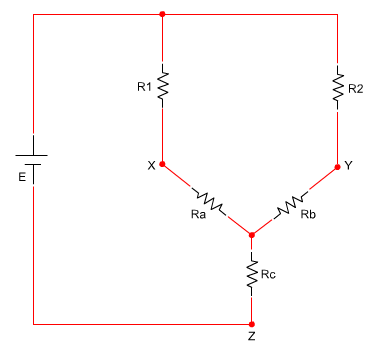
איור 6.3

אפשר לראות שבמעגל זה אכן אפשר לפשט את נגדי המעגל ולחשב את ההתנגדות השקולה ש"רואה" מקור המתח. כלומר, שלא כבמעגל המקורי, אפשר למצוא בו קבוצת נגדים בחיבור טורי או מקבילי.

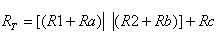
חשוב לציין שהפוטנציאל בנקודות השונות x,y ו-z זהה בשני המעגלים (לפני ההמרה ואחרי ההמרה).