קורס בתורת החשמל מאת יוסי יאשי

תרגיל דוגמה 1

נתון המעגל החשמלי שבאיור 5.9:

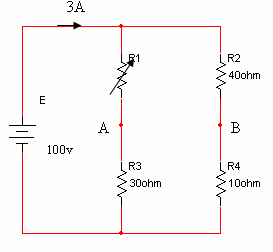
איור 5.9

חשבו את:

א.    ערך הנגד R1

ב.     הפרש המתחים ABU

ג.       לאיזה ערך יש לשנות את הנגד R1 כך שהפרש המתחים בין הנקודות  A ל- B יתאפס?

פתרון תרגיל דוגמה 1

א.  נחשב את הזרם בענף הימני:

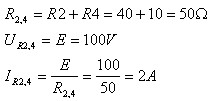
נעזר בחוק הזרמים של קירכהוף:

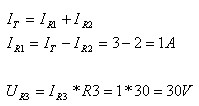
על פי חוק המתחים של קירכהוף: 

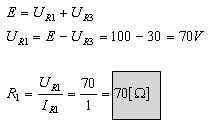
ב.  נקבע תחילה את קוטביות מפלי המתח על הנגדים– ראו איור 5.10 .

דרך הנגדים R1 ו- R2 הזרם יורד, לכן כיוון חצי המתח על הנגדים האלה הוא כלפי מעלה.

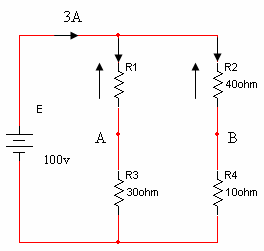
איור 5.10

את המתח ABU אפשר לחשב באמצעות איסוף המתחים מנקודה A ל- B. למשל:

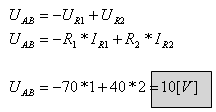
ג.  בסעיף זה מבקשים מאתנו להביא את הגשר למצב של איזון, כלומר מצב שבו הפוטנציאל בנקודה A שווה לפוטנציאל בנקודה B.

תרגיל דוגמה 2

הנגד (q(R5 שמופיע במעגל שבאיור 5.11 הנו נגד המשנה את התנגדותו כתוצאה משינויי טמפרטורה, על פי המשוואה :

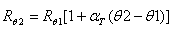
בטמפרטורה של C °55 מד הזרם מראה קריאה של 0.4A - התנגדותו של (q)5R בטמפרטורה זו Ω20 ומקדם הטמ"פ של הנגד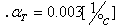 

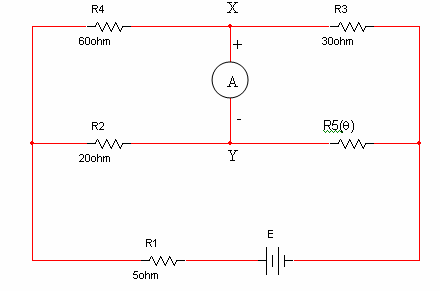
איור 5.11

חשבו את:

א.     מקור המתח E

ב.      הטמפרטורה שבה צריך להיות (R5(q כך שמד הזרם יראה אפס.

פתרון תרגיל דוגמה 2

א.  מאחר שאין התייחסות למד הזרם, אנו נניח כי מדובר במד זרם אידאלי, לכן נסרטט במקומו חוט קצר.

היות שקריאת מד הזרם שלילית באותו חוט קצר (מד זרם), הזרם עובר מנקודה Y לנקודה X (נכנס בהדק ה – ויוצא בהדק ה + של מד הזרם ).

בטמפרטורה של 55°C המעגל נראה כך:

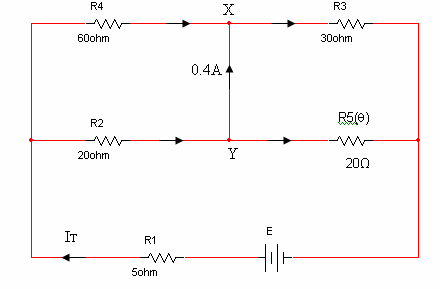
נחשב את ההתנגדות השקולה ש"רואה" מקור המתח:

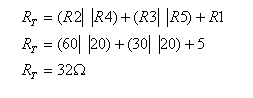
כדי לחשב את מתח המקור יהיה עלינו למצוא את הזרם הכללי במעגל.

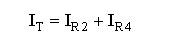
מאחר שהנגדים R2 ו- R4 מחוברים במקביל אפשר באמצעות כלל מחלק הזרם למצוא את יחס הזרמים ביניהם. כך גם לגבי הנגדים R3 

ו-(R5(q

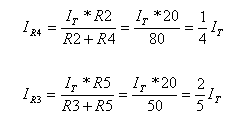
נעזר בחוק הזרמים של קירכהוף למציאת הזרם הכללי:

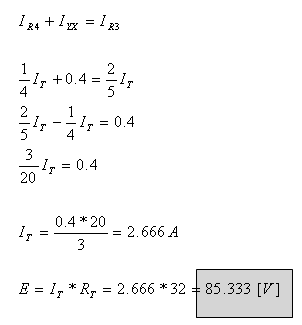
ב.  מד הזרם יראה אפס רק כשהגשר יהיה מאוזן. לכן בשלב ראשון נמצא את ערכו של הנגד (R5(q שיביא לאיזון הגשר:

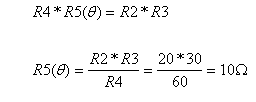
התנגדות זו מתייחסת להתנגדות לאחר שינוי הטמפרטורה (במקרה זה לאחר קירור הנגד), לכן את הטמפרטורה שבה מצוי המעגל כשגשר מאוזן נחשב כך:

כעת נחשב את הטמ"פ שגרמה להתנגדות זו:

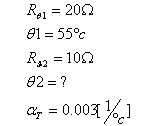
מאחר שמקדם הטמפרטורה אינו נתון בטמפרטורה מסוימת, השימוש במשוואת הנגד התלוי בטמפרטורה יהיה פשוט יותר (כפי שהוזכר בפרק 2):

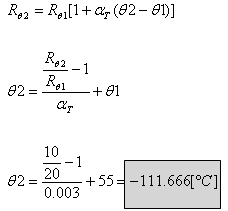
תרגיל דוגמה 3

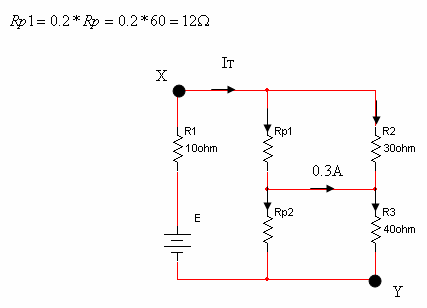
במעגל שבאיור 5.12 מחובר פוטנציומטר שערכו המרבי הנו W60.

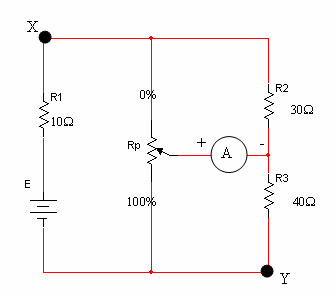
איור 5.12.

א. קבעו מה צריך להיות מצב הזחלן באחוזים כך שמד הזרם יראה אפס.

ב. משנים את מצב הזחלן כך שהוא מצביע על 20% מערך הפוטנציומטר. במצב זה קריאת מד הזרם היא

  0.3A. חשבו את גודל מקור המתח.

ג. מחברים בין הנקודות X  ו- Y מד מתח. רשמו מה תהיה קריאתו.

פתרון תרגיל דוגמה 3

א.  מאחר שאין אנו יודעים את מיקום הזחלן, נניח שערכו העליון של הפוטנציומטר הוא X אוהם. לכן ערכו התחתון יהיה  (60-X) אוהם.

במצב שבו מד הזרם מראה אפס, אפשר לומר שהגשר מאוזן ולכן מתקיים התנאי:

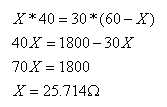
מצב הזחלן באחוזים:

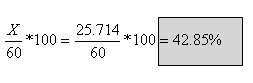
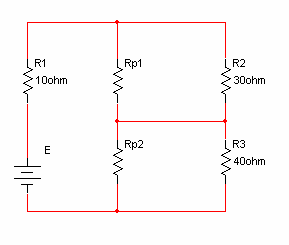
ב.  במצב שבו הזחלן מצביע על 20% מערך הפוטנציומטר, נקבל שערכו של הנגד העליון Rp1 :

יש לשים לב שמגמת מד הזרם היא ימינה מכיוון שקריאתו הייתה חיובית, כלומר כיוון הזרם במצב הזה הוא מם הפלוס למינוס של מד הזרם.

על פי חוק הזרמים של קירכהוף:

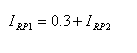
נבטא את הזרמים דרך  RP1 ו- RP2 אמצעות כלל מחלק הזרם:

ג.  חיבור מד המתח בין הנקודות  X  ו- Y לא ישנה את תוצאות המעגל משום שהוא מהווה נתק (התנגדות אינסופית). כלומר אפשר להתבסס על המעגל שנתון בסעיף ב ולחשב בו את המתח שבין הנקודות X ו- Y:

                                                                    סוף פרק 5

•    הקודם                                                                                                                   
• המשך לתרגילים מסכמים לפרק 5