קורס בתורת החשמל מאת יוסי יאשי

תרגיל דוגמה 24

ערכו של הנגד המשתנה שמחובר במעגל שבאיור 3.34 הוא W50. הזחלן C מצוי באמצע הנגד המשתנה.

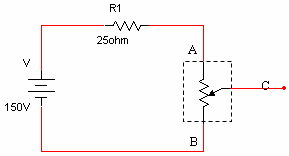
איור 3.34

חשבו את:

א. המתח בין הנקודות C ו- B;

ב. ההספק ש"מתבזבז" בפוטנציומטר;

ג. משנים את מצב הזחלן, כך שהוא מצוי בנקודה A. חזרו על סעיפים א ו- ב.

פתרון תרגיל דוגמה 24

לצורך הפתרון, נחלק את הנגד המשתנה לשני נגדים כמתואר באיור שלפניכם:

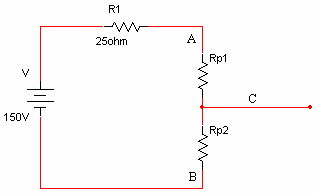
א. המעגל שמתקבל הנו מעגל טורי, ולכן נחשב את הזרם במעגל כך:

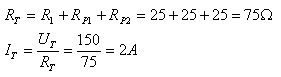
חישוב המתח בין הנקודות CB:

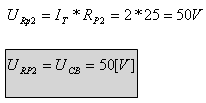
ב. ההספק ש"מתבזבז" בפוטנציומטר הוא סכום ההספקים על שני נגדיו. מאחר שהם מחוברים בטור (זורם דרכם הזרם הכללי), אפשר לחשב את הספק הזה גם כך:

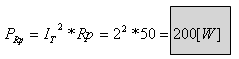
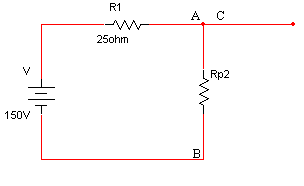
את המעגל במצב הזה אפשר לתאר שוב כמעגל טורי, אך הפעם, הנגד p1R שווה לאפס, ואילו הנגד p2R שווה ל- W50 . לכן בסרטוט אפשר למחוק את p1R (הופך לחוט קצר – התנגדות אפסית):

את המתח בין הנקודות CB נחשב כך:

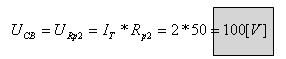
תרגיל דוגמה 25

ערכו של הפוטנציומטר שמחובר במעגל הוא W80

בתרגיל זה הזחלן C ניתן להזזה, רק אחרי סגירת מתג ההפעלה.

א. כוונו את הזחלן, כך שההתנגדות בין הנקודות AC תהווה 25% מערכו.

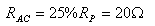
חשבו את:

1.       הזרם שמספק מקור המתח;

2.       המתח שבין הנקודות CB;

3.       ההספק המתפתח בנגד R3.

פתרון תרגיל דוגמה 25

לצורך החישובים אפשר לתאר את המעגל כך:

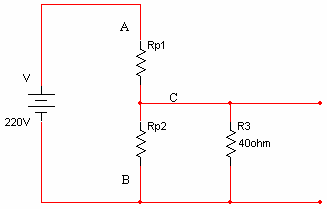
נחשב את ההתנגדות השקולה שרואה מקור המתח:

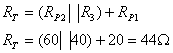
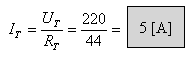
נעזר בכלל מחלק בזרם:

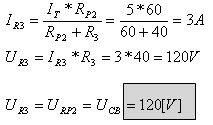
חישוב ההספק בנגד R3:

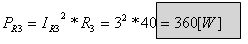
ב. סגרו את המתג S, והשווו בין תוצאות החישוב לתוצאות הנמדדות. 

ג. כתוצאה משינוי מצב הזחלן, עצמת הזרם עולה. האם תזוזת הזחלן הייתה ימינה על גבי הציר או שמאלה?

  הזיזו את מצב הזחלן והיווכחו בטענתכם.

ד. כוונו את הזחלן לאמצע בדיוק ורשמו את קריאת המתח UCB. האם המתח בין הנקודות CB שווה למחצית מתח המקור?

הזיזו את מצב הזחלן והיווכחו בטענתכם.

ה. אם ננתק את הנגד R3 מהמעגל. האם המתח בין הנקודות CB יהיה שווה למחצית מתח המקור?

לחצו על  להוצאת הנגד R3 מהמעגל והיווכחו בטענתכם.

ו. החזירו את הנגד R3 למעגל על ידי לחיצה נוספת על . באיזה מצב צריך להיות הזחלן, כך שההספק בנגד R3 יתאפס?

הזיזו את מצב הזחלן והיווכחו בטענתכם.

ז. כוונו את הזחלן, כך שההתנגדות בין הנקודות AC תהווה 50% מערכו.

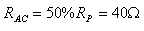
וחשבו את המתח בין הנקודות CB. הזיזו את מצב הזחלן והיווכחו בטענתכם.

ח. במידה וננתק את הנגד R3 מהמעגל. האם המתח בין CB ישתנה? אם כן מה יקרה לו – יעלה או ירד?

לחצו על  להוצאת הנגד R3 מן המעגל והיווכחו בטענתכם.

תרגיל דוגמה 26

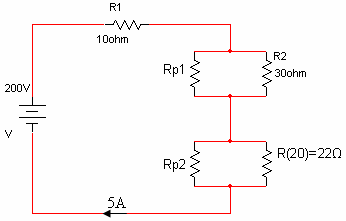
נתון מעגל חשמלי כמתואר באיור 3.35. כתוצאה ממצב הזחלן C, החלק  העליון של התנגדות הנגד המשתנה הוא בעל ערך של 20% מערכו הכולל.

הנגד (q)R הוא נגד המשנה את התנגדותו כתוצאה משינויי טמפרטורה, על פי המשוואה

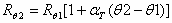
בטמפרטורת החדר (C°20) התנגדותו של (q)R שווה 22Ω.

מקדם הטמפרטורה של הנגד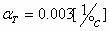 

הזרם שיוצא ממקור המתח בטמפרטורת  החדר כתוצאה ממצב זה הוא 5A.

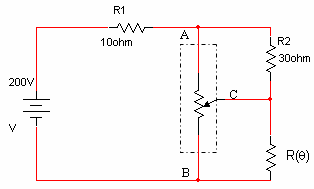
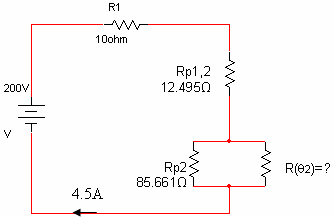
איור 3.35     

חשבו את:

א. ערכו של הפוטנציומטר Rp;

ב. ההספק המתפתח בפוטנציומטר בטמפרטורת  החדר;

ג. באיזו טמפרטורה  צריך להימצא המעגל, אם ידוע שעוצמת הזרם הכללית ירדה ב- 10% מערכה בטמפרטורת  החדר?

פתרון תרגיל דוגמה 26   

כדי לפתור תרגילים המשלבים פוטנציומטר, מומלץ מאוד לסרטט מעגל חדש, המחלק את הפוטנציומטר לשני נגדים. על מעגל זה, נציב את הנתונים הידועים בטמפרטורת  החדר.

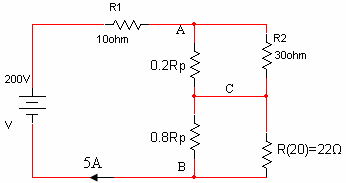
א. נחשב את ההתנגדות השקולה של המעגל:

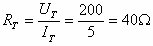
נבטא התנגדות זו כתלות בנגדי המעגל:

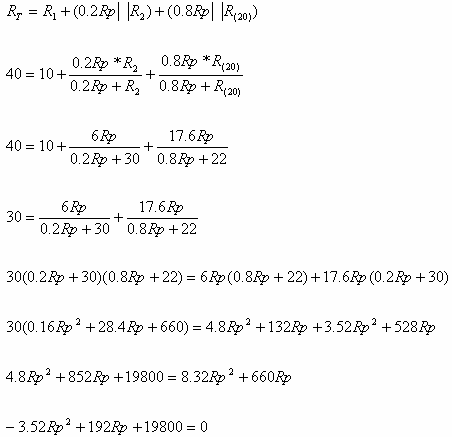
התקבלה משוואה ריבועית לנגד Rp ולה שני שורשים (פתרונות):

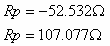
לא קיימת התנגדות שלילית ולכן גודלו של הפוטנציומטר:

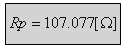
ב. כדי לחשב את ההספק הכולל בפוטנציומטר, עלינו לחשב את ההספק על כל אחד מחלקיו  לחוד (גם העליון וגם התחתון), כי אין הם מחוברים בטור (הזרם דרכם אינו אותו הזרם).

נגדיר תחילה את נגדי הפוטנציומטר:

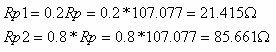
נעזר בכלל מחלק הזרם:

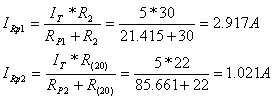
את ההספק של הפוטנציומטר נחשב כאמור כך:

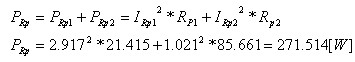
נסרטט שוב את המעגל, אך הפעם עם הנתונים השייכים לטמפרטורה q כלשהי:

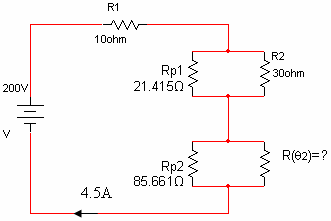
נחשב תחילה את התנגדותו של הנגד המשתנה (q)R בטמפרטורה הלא ידועה 2q.

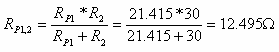
נסרטט שוב מעגל חדש:

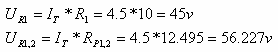
על פי חוק המתחים של קירכהוף:

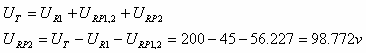
חישוב הנגד התלוי בטמפרטורה:

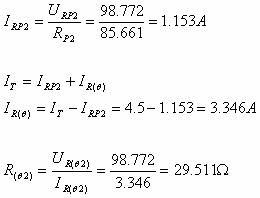
כעת נחשב את הטמפרטורה שגרמה להתנגדות זו:

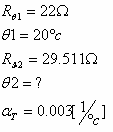
מאחר שמקדם הטמפרטורה אינו נתון בטמפרטורה מסוימת, השימוש במשוואת הנגד התלוי בטמפרטורה יהיה פשוט יותר (כפי שהוזכר בפרק 2):

 סוף פרק 3

•    הקודם                                                                                                     
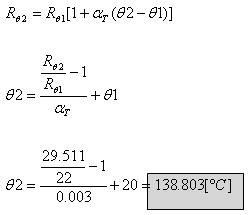
• המשך לתרגילים מסכמים לפרק 3